공부를 하고 정리하는 것이 매우 중요하다. 근데 그 정리를 하기가 조금 귀찮은 것이 아니다. 앞으로는 그 때 그 때 정리하도록 하고, 모아두지 말아야겠다.. 업로드 할 것이 한 두 가지가 아니다ㅜㅜ
자료구조 공부의 순서에 상관없이 그냥 올리려고 한다.
오늘은 우선 순위 큐를 위한 Heap 자료 구조에 대해서 정리한다. 큐 형태로 포장하지 않았을 뿐이지, 큐를 염두하여 만들었기 때문에 큐라고 이름만 바꾸면 우선 순위 큐가 될 수 있다.
Heap 이란 무엇인가?
힙이란 다음 그림과 같은 형태이다.

Q : 엥? 이건 (완전) 이진 트리가 아닌가?
A : 그렇다. 맞다
- 빼박 이진 트리 아닌가? 의미의 '완전'이 아니다, 리프 노드를 제외한 모든 노드들은 두 자식 노드를 꼭 채워진 형태의 트리, 리프 노드는 꼭 왼쪽부터 채워지는 트리를 의미하는 '완전 이진 트리'
이 친구들은 이진 트리의 형태를 하고 있으나, 일반 이진 트리와는 달리 좀 많은 규칙들로 탄탄히 채워진 트리이다. 이 규칙들을 통해 힙의 특징을 설명할 것이다.
Heap 의 특징
1. 완전 이진 트리의 특성을 갖는다.
리프 노드를 제외한 모든 노드들은 두 자식 노드를 모두 채운 상태여야하며, 리프 노드는 채울 때, 왼쪽부터 채워져야 한다.
2. 자식 노드와 부모 노드 간의 규칙이 존재한다.
힙은 밑에서 부터 쌓아 올리는 자료 구조이기 때문에 부모 노드와 자식 노드 간 특정한 규칙이 존재한다. 예를 들어, 자식 노드는 부모보다 커야만 한다, 자식 노드는 부모보다 작아야만 한다 등의 규칙이다.

3. 일반적인 트리와 달리, 왼쪽 자식과 오른쪽 자식은 부모 노드 기준으로 값이 작은 노드와 큰 노드로 취급하지 않는다.
그저 리프 노드의 자식을 채울 때, 왼쪽에서 오른쪽 순으로 먼저 채우는 것 뿐이다.
힙 구조에 값을 삽입
트리의 가장 끝에 삽입 후 부모와 비교하여 위치를 조정한다.

힙 구조에서 값을 삭제
삭제할 때에는 탐색 후 삭제가 아니라, Pop의 개념이다. 루트 노드의 값을 빼준다. 그리고 나서 꼭 트리를 재구성 해줘야하는데 이 때, 루트를 어떤 값으로 채울 것인가에 대한 고민을 해야한다. 그러기 위해서는 가장 마지막 노드를 루트에 넣고 트리를 재구성하여 내려간다.

이와 같은 구조에서 3을 제거하고, 10을 루트에 넣어본다.

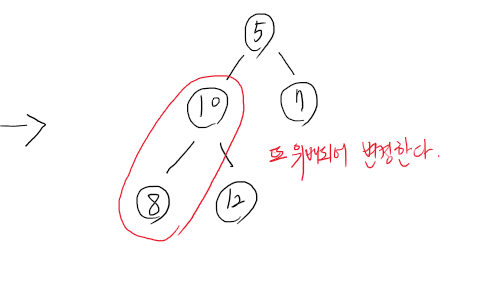
10을 루트에 넣고 보니 위배되는 부분들이 존재한다. 이를 풀기 위해 계속 구조를 재조정한다.

이 값을 삭제하는 부분으로 인해 우선 순위 큐의 구현이 가능하다!!!
우선 순위 큐란 무엇인가? 우선 순위가 높은 것을 먼저 빼는 것이다. 큐의 선입선출 이딴 거 다 필요없고, 언제 들어가든 간에 우선 순위가 높은 것이 먼저 나오는 것이다.
단, 우선 순위가 같은 경우에는 선입선출이 보장되어야 한다. 이는 리프노드의 왼쪽 삽입 우선 특징(1번 특징)으로 인해서 같은 우선 순위의 경우 선입 선출을 보장하도록 프로그램을 작성할 수 있다.
즉, 힙의 루트 노드는 삽입, 삭제 과정에서의 힙 자료구조의 재조정을 통해 각 힙에서 지정한 규칙에 의거하여 우선 순위가 높은 값으로 채워넣어진다.
예를 들어
Max Heap의 경우에는 루트 노드로 올라갈수록 값이 커짐 -> 큰 값일 수록 우선 순위가 높다.
Min Heap의 경우에는 루트 노드로 올라갈수록 값이 작아짐 -> 작은 값일 수록 우선 순위가 높다.
사용자 정의 Heap의 경우에는 구조체 등을 이용하여 우선 순위 변수를 따로 두고 진행한다면 이 또한 우선 순위를 매길 수 있다.
이렇게 힙 구조에서 루트 노드에서 값을 빼냄으로써 우선 순위대로 값을 취할 수 있기 때문에 heap을 통한 우선 순위 큐를 구현할 수 있는 것이다.
힙의 구현
힙을 구현할 때에는 배열로 구현할 것이다. 왜냐?
그 이유를 알기 이전에 있어서 힙을 어떤 자료 구조로 구현할 수 있는지부터 확인해보자.
1. 완전 이진 트리이므로, 연결 리스트의 구조로 당연히 구현이 가능하다.
2. 그리고 인덱스 조절을 통한 배열로도 가능하다.
그렇다면 왜 배열로 구현할 것인가?
우리는 삽입 연산을 진행할 때, 트리의 가장 마지막 노드 자리에 값을 삽입한다. 만약 단순 연결 리스트로 구현했다면 이 마지막까지 순회하기에 비용이 많이 든다. 그리고 부모, 자식 간의 노드 비교가 많기 때문에 비교적 비용이 적게 드는 랜덤 엑세스가 가능한 배열로 구현하기로 했다. (라고 윤성우 교수님의 자료구조 서적에 나와있다 ㅋ)
그래서 인덱스 제어 방법이 필요하다.
1. 배열의 인덱스는 1부터 시작한다. ( 인덱싱을 용이하게 하기 위함이다. 구현하다보면 안다. 왜 인덱싱을 1부터 하는지 ㅋㅋㅋ)
2. 현재의 인덱스를 넣었을 때, 부모 혹은 자식의 노드를 구하는 방법을 알아야 한다.

위 그림과 같이 계산하면 임의의 인덱스를 기준으로 부모 노드의 인덱스를 구할 수도, 자식 노드를 구할 수 도 있다. 즉, 완전 이진 트리 구조라고 할지라도 인덱스를 통한 랜덤 엑세스가 가능한 것이다.
아래는 그 코드와 주석이다.
---
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
|
#include <stdio.h>
#define TRUE 1
#define FALSE 0
#define HEAP_LEN 100
struct heap_element // 정수 값을 저장하는 힙의 노드 구조체로 우선 순위를 지정할 수 있다.
{
int priority; // 값이 작을수록 우선 순위가 크다.(1등 ~ 10등 ... 개념의 수를 저장함)
int data;
};
typedef struct heap_element heap_element;
struct heap
{
int count;
heap_element heap_arr[HEAP_LEN]; // 힙은 배열 구조를 기반으로 구현된다.
};
typedef struct heap heap;
void HeapInit(heap* h);
int HIsEmpty(heap* h);
void HInsert(heap* h, int data, int priority);
int HDelete(heap* h);
void ShowHeap(heap* h);
int GetParentIndex(int child_index);
int GetLeftChildIndex(int parent_index);
int GetRightChildIndex(int parent_index);
int GetChildIndex(heap* h, int parent_index);
int main(void)
{
heap h;
HeapInit(&h);
HInsert(&h, 3, 1);
HInsert(&h, 5, 2);
HInsert(&h, 10, 5);
HInsert(&h, 8, 4);
HInsert(&h, 12, 6);
HInsert(&h, 7, 3);
printf("%d \n", HDelete(&h));
ShowHeap(&h);
printf("--- Del --- \n");
while (!HIsEmpty(&h))
printf("%d, ", HDelete(&h));
fputc('\n', stdout);
ShowHeap(&h);
return 0;
}
void HeapInit(heap* h)
{
int i = 0;
h->count = 0;
for (i = 0; i < HEAP_LEN; i++)
{
h->heap_arr[i].data = 0;
h->heap_arr[i].priority = -1;
}
return;
}
int HIsEmpty(heap* h)
{
return (h->count == 0) ? TRUE : FALSE;
}
void HInsert(heap* h, int data, int priority)
{
int insert_index = h->count + 1;
int parent_index = 0;
heap_element new_element = { priority, data };
while (insert_index != 1) // 처음 삽입되는 위치가 루트 노드가 아니면 혹은 갱신된 추가 인덱스가 루트 노드가 아니면
{
parent_index = GetParentIndex(insert_index);
if (new_element.priority >= h->heap_arr[parent_index].priority) // 우선 순위가 부모가 높다면 구조 재조정이 필요 없다.
break;
else // 추가할 노드가 우선 순위가 높은 경우, 계속 구조 재조정이 필요함.
{
h->heap_arr[insert_index] = h->heap_arr[parent_index];
insert_index = parent_index;
}
}
h->heap_arr[insert_index] = new_element;
h->count++;
return;
}
int HDelete(heap* h)
{
int r_data = h->heap_arr[1].data; // 삭제할 데이터(Pop 할 데이터와 같은 의미)
heap_element last_element = h->heap_arr[h->count]; // 비교 대상인 마지막 노드 지정( 마지막 노드를 루트 자리로 올려 비교하기 때문 )
// 최종 결정된 인덱스
int parent_index = 1; // 루트 노드 부터 시작한다.
int child_index = 0;
while (child_index = GetChildIndex(h, parent_index))
{
if (last_element.priority <= h->heap_arr[child_index].priority) // 자식 노드보다 우선 순위가 높다면 현재 구한 인덱스로의 변경만 하면 된다.
break;
else // 계속해서 구조의 재조정이 필요한 경우
{
h->heap_arr[parent_index] = h->heap_arr[child_index];
parent_index = child_index;
}
}
h->heap_arr[parent_index] = last_element;
h->count--;
return r_data;
}
// Heap의 내용을 트리의 계층(레벨) 별로 보여준다.
void ShowHeap(heap* h)
{
int begin = 1, end = 1, index = 1;
int i = 0;
if (h->count == 0)
{
printf("heap이 비었습니다!\n");
return;
}
printf("%d(%d), \n", h->heap_arr[1].data, h->heap_arr[1].priority);
while (index <= h->count)
{
begin = GetLeftChildIndex(begin), end = GetRightChildIndex(end); // 각 레벨 층의 시작과 끝 인덱스 설정 후 출력한다
if (end > h->count) end = h->count; // end가 마지막 노드보다 넓은 범위에 있다면 end를 마지막 노드의 인덱스로 설정
index = end + 1; // 위에서 지정한 end 다음 값으로 변경한다.
for (i = begin; i <= end; i++)
printf("%d(%d), ", h->heap_arr[i].data, h->heap_arr[i].priority);
fputc('\n', stdout);
}
return;
}
// 부모 노드의 인덱스를 구한다.
int GetParentIndex(int child_index)
{
return child_index / 2;
}
// 왼쪽 자식 노드의 인덱스를 구한다.
int GetLeftChildIndex(int parent_index)
{
return parent_index * 2;
}
// 오른쪽 자식 노드의 인덱스를 구한다.
int GetRightChildIndex(int parent_index)
{
return (parent_index * 2) + 1;
}
// 두 자식 노드 중 우선 순위에 따라 반환한다.
int GetChildIndex(heap* h, int parent_index)
{
if (GetLeftChildIndex(parent_index) > h->count) // 자식 노드가 없으면 0 반환
return 0;
else if (GetLeftChildIndex(parent_index) == h->count) // 자식 노드가 하나인 경우에는 해당 인덱스 반환
return GetLeftChildIndex(parent_index);
else // 두 자식 노드 중 우선 순위가 높은 것의 인덱스 반환
{
int left_child_index = GetLeftChildIndex(parent_index), right_child_index = GetRightChildIndex(parent_index);
if (h->heap_arr[left_child_index].priority > h->heap_arr[right_child_index].priority) // 오른쪽 자식 노드가 더 우선 순위가 높다면
return right_child_index; // 오른쪽 자식 노드의 인덱스 반환
else // 왼쪽 자식 노드가 더 우선 순위가 높거나 양쪽 노드의 우선 순위가 같다면
return left_child_index; // 왼쪽 자식 노드의 인덱스 반환
}
}
|
cs |
---

'프로그래밍응용 > C 자료구조' 카테고리의 다른 글
| C Data Structure - 버블 정렬 (0) | 2021.01.03 |
|---|---|
| C Data Structure - 단순 배열 리스트 (0) | 2021.01.03 |
| C Data Structure - 재귀를 통한 이진탐색 구현해보기 (0) | 2020.09.08 |
| C Data Structure - 재귀를 통한 피보나찌 수열 구하기 (0) | 2020.09.08 |
| C Data Structure - 이진 탐색 (0) | 2020.09.07 |