이번에는 병합 정렬이다. 이게 생각보다 간단하긴 한데 복잡하다(?) 일단 시작한다.
병합 정렬이란?
병합 정렬의 기본은 다음과 같다.
1. 배열을 원소 단위로 쭉~~ 나눴다가
2. 다시 단계적으로 정렬과 동시에 결합을 반복한다.
그림으로 나타내자면 다음과 같다.


그럼 문제는 무엇이냐? 어떻게 쪼갤 것인가? 이다. arr[0] , arr[1] 이게 쪼갠 것 아닌가? 아니다. 그냥 원소에 접근한거지 쪼갠게 아니다.
그럼 쪼갠다 라는 의미를 아주 곰곰히 생각해봐야한다.
쪼갠다는 것은 큰 덩어리부터 시작해서 작은 단위로 나눈다는 것이고, 내가 원소 레벨까지 쪼갰다 라는 의미는 내가 지금 쪼개고 있는 진행 흐름이 원소 단위까지 접근했다! 라는 것이다.
좀 어렵지만 잘 생각해라. arr[0] 에 접근하는 것은 우리 집 강아지와 할머니도 할 수 있는 행위이다.(집에 강아지와 할머니는 없다) 이것은 쪼갠 것이 아니고 접근한 거다.
쪼갠다는 것은 그림의 설명과 같다.
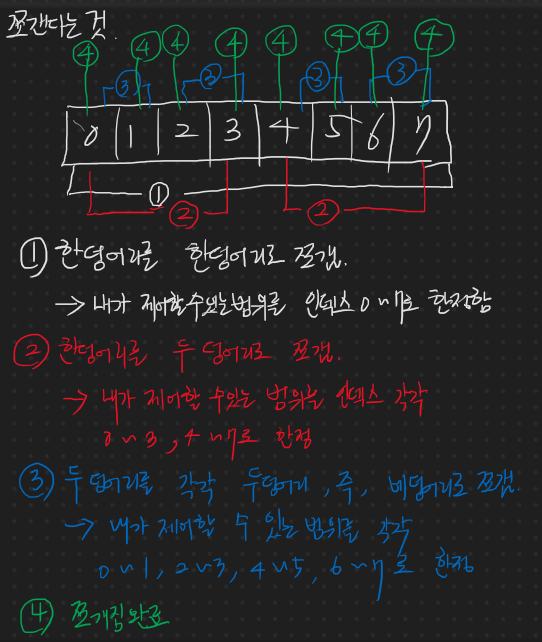
제어할 수 있는 인덱스 범위를 한정지으면 되겠다 이것이다. 그런데 내가 가만히 보니 이 쪼개는 단계가 범위만 줄어드는 것 외에는 모두 같은 짓을 하고 있는 것이다. 그렇다면 원본 배열을 던지고, 그와 함께 범위 값만 다르게 던져주면 알아서 쪼개주는 함수가 없으려나?
있다. 바로 재귀 함수이다. 바로 코드를 본다

위 함수처럼 원본과 범위를 지정하여 함수에 던져주면 알아서 반으로 쪼갤 것이다.
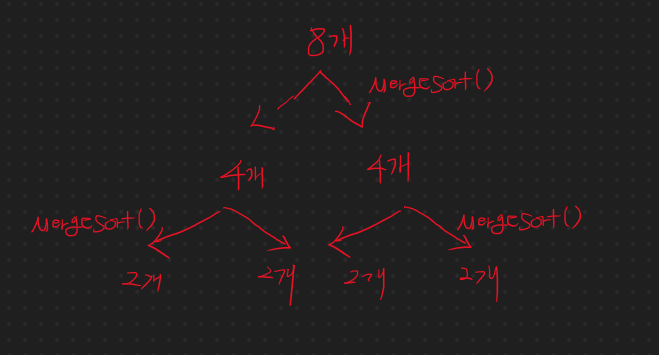
위 그림처럼 될 것이다.
그렇다면 쪼갰으니 정렬과 결합을 해야한다. 다시 MergeSort 코드를 보겠다.

MergeSort는 범위를 나누어 두 토막 내고(2개의 MergeSort) 그리고 정렬과 결합을(Merge) 수행한다 라는 사실을 기억해야하며, 신뢰해야한다. 그니까 밑에 잔뜩 실행된 MergeSort 함수는 신경쓰지말고, 현재 주어진 범위들에 대해서 정렬하고 결합한다는 것이다.

위 그림처럼 밑 바닥까지 MergeSort 하면서 내려가면 더 이상 쪼개지 못하므로 각 MergeSort에게 지정된 범위에 대해서 Merge 를 통해 정렬과 결합을 수행해주고 리턴한다 그러면 한 단계 위층에서의 MergeSort들은 내부적으로 정렬된 두 덩어리를 받을 것이고 또한 그들도 Merge 를 통해 정렬과 결합을 수행해주고 리턴해준다. 언제까지? 다 합쳐질 때까지!
물론!!!! 여기서 정렬은 조상님이 와서 대신 해주는게 아니다! Merge라는 함수 내에서 이를 구현해야한다. 이는 어렵지 않으므로 코드로 확인해보면 될 것이다.

이 코드가 핵심인데, 앞 범위 토막과 뒷 범위 토막의 요소들을 모두 둘둘씩 비교하여 작은 값을 새로운 공간에 차곡차곡 넣는 방식이다. 이게 가능한 이유는 각 토막들은 아래 계층에서 이미 정렬되어 올라왔기 때문이다! (쓰면서 명확히 깨달음 ㅋ)

내가 무슨 말을 하고 있는지 모르겠다면 직접해봐라 미래의 나야
코드 및 실행 결과
----
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
#include <stdio.h>
#include <stdlib.h>
void ShowArray(int arr[], int n)
{
int i = 0;
for (i = 0; i < n; i++)
printf("%d ", arr[i]);
fputc('\n', stdout);
return;
}
void Merge(int arr[], int begin, int mid, int end)
{
int bidx = begin, eidx = mid + 1, cidx = 0, lidx = -1; // begin side index, end side index, current index, last index
int* temp = (int*)malloc((end - begin + 1) * sizeof(int)); // 필요한 만큼만 할당한다.
while (bidx <= mid && eidx <= end)
{
if (arr[bidx] <= arr[eidx])
temp[cidx++] = arr[bidx++];
else
temp[cidx++] = arr[eidx++];
}
if (bidx > mid) // end side는 아직 다 안 채웠음.
lidx = eidx;
else if (eidx > end) // begin side는 아직 다 안 채웠음.
lidx = bidx;
// 아직 정렬되지 않은 side를 채워넣는다.
while (cidx < (end - begin + 1))
temp[cidx++] = arr[lidx++];
// 원래 배열의 해당 인덱스 구간에 정렬된 결과를 반영한다.
for (lidx = begin, cidx = 0; lidx <= end; lidx++, cidx++)
arr[lidx] = temp[cidx];
ShowArray(arr, 21);
free(temp);
return;
}
void MergeSort(int arr[], int begin, int end)
{
int mid = (begin + end) / 2;
if (begin < end) // 아직 나눌 수 있음.
{
MergeSort(arr, begin, mid);
MergeSort(arr, mid + 1, end);
Merge(arr, begin, mid, end);
}
// 나눌 수 없는 경우는 원소 하나 단위이니 할 수 있는게 없다 -> 그냥 리턴
return;
}
int main(void)
{
int arr[21] = { 20, 19, 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0 };
int i = 0;
ShowArray(arr, 21);
MergeSort(arr, 0, 20);
printf("최종 정렬 결과 : \n");
ShowArray(arr, 21);
return 0;
}
|
cs |
----

머리가 참 아득해진다..
머리가 아득해지는 김에 빅오를 보자
병합 정렬 성능
최악/ 평균 / 최선에 상관없이 비교와 데이터 이동 연산을 모두 세어보면 O(n log 2 n)이다. 2는 아래 첨자 2이다.
'프로그래밍응용 > C 자료구조' 카테고리의 다른 글
| C Data Structure - 퀵 정렬 (0) | 2021.01.06 |
|---|---|
| C Data Structure - 스택 - 잃어버렸던 포스팅.. (0) | 2021.01.05 |
| C Data Structure - 힙 정렬 (0) | 2021.01.05 |
| C Data Structure - 연결 리스트 (0) | 2021.01.04 |
| C Data Structure - 삽입 정렬 (0) | 2021.01.04 |