C Data Structure - 이진 탐색 트리 1
오늘은 이진 탐색 트리이다. 이전까지는 선형 자료 구조를 공부했었다. 뭐 예를 들어, 일반 배열 리스트, 연결 리스트, 스택, 큐 등의 선형 구조만 포스팅했는데, 드디어! 비 선형 자료 구조이다.
typingdog.tistory.com
여기에 이어서 이진 탐색 트리에 대해서 분석하고 기록할 것이다.
준비 및 구성
먼저, 이전 포스팅에서의 개념과 조건들을 토대로 어떻게 준비할 것인가이다!
트리 구성의 준비물이 되는 노드이다! 노드의 구성은 다음과 같다.

크게 설명할 것이 없다. 이 노드 구조체를 통해서 값과 이진 탐색 트리 조건에 맞는 자식 노드를 가리킬 포인터 2개의 구성이 끝인 것이다.
이런 구조체로 노드를 생성할 때에는 꼭 다음과 같은 상태로 초기화되는 것이 보장되어야 한다.

트리에 접근하는 방법(루트 노드에 접근하는 방법)
삽입 연산을 하기 이전에 트리에 접근할 때에는 무조건 루트 노드부터 접근을 시작해야한다. 그 루트 노드로의 접근을 어떤 식으로 할 수 있는지, 그 루트 노드를 어떻게 정하는지를 기록한다.

위 코드는 메인 함수 내에서 실행되는 코드로 root 라고 하는 포인터로 트리의 루트 노드를 가리키도록 설계해놓았다.
트리에 노드 삽입 연산
먼저, 삽입 연산은 그림으로 나타냈을 때, 아래와 같다.

위 삽입 연산에 해당되는 코드를 함께 보는게 좋을 것 같다.
먼저, 트리에 노드가 0개 일 때 의 노드 생성이다.

트리에 노드가 1개 이상일 경우에는 다음처럼 삽입 연산을 수행한다.

트리 순회 연산
트리에 노드를 추가만 해서는 뭘 하는가! 순회도하고 탐색도 할 수 있어야, 탐색 트리이지. 먼저, 순회 연산에 대해 알아본다.
하.. 일단(ㅋ) 순회 연산은.. 여러 종류가 있다. 이 여러 종류의 연산 과정을 내 블로그 내에서 최초 도입한 신개념 비디오 장치를 통해 촬영된 것을 올릴 것이다.
일단 트리에서의 순회는 조금 특이하다.
첫 노드인 루트 노드를 기준으로 한 큰 트리가 존재하지만, 첫 노드의 자식을 기준으로 또 하나의 서브 트리가 존재한다. 이 서브 트리를 하나의 대상으로 연산이 이루어지고, 또 그 자식 노드를 기준으로 또 서브 트리가 존재하며 단말 노드가 될 때까지 서브 트리 군이 형성된다. -> 재귀적으로 문제를 풀 수 있다는 것이다.
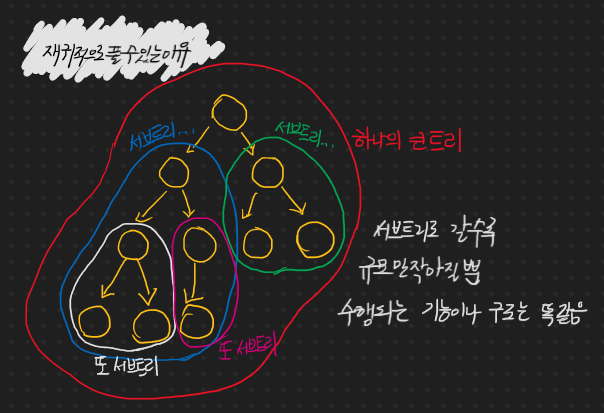
그래서 이 순회에서는 재귀를 통해 순회를 진행할 것이다. 삭제 또한 마찬가지이나 다양한 방법들을 넣기 위해서 순회에만 재귀를 적용하도록하고, 삭제에서는 반복문을 통해 삭제를 진행한다.
전위 순회 : 루트 노드를 기준으로 먼저 루트 노드의 값을 읽고, 그 다음 순차적으로 왼쪽 트리를 방문하고, 그 뒤에 오른쪽 트리를 방문하는 방법이다.
서브 트리의 루트 방문(값 Get) -> 왼쪽 링크를 통한 왼쪽 서브 트리 방문 -> 오른쪽 링크를 통한 오른쪽 서브 트리 방문

중위 순회 : 루트 노드를 기준으로 먼저 왼쪽 트리를 방문하고, 그 다음 해당 루트 노드의 값을 읽고, 그 다음 오른쪽 트리를 방문하는 방법이다.
왼쪽 링크를 통한 왼쪽 서브 트리 방문 -> 서브 트리의 루트 방문(값 Get) -> 오른쪽 링크를 통한 오른쪽 서브 트리 방문

후위 순회 : 루트 노드를 기준으로 먼저 왼쪽 트리를 방문하고, 그 다음 오른쪽 트리를 방문한 뒤에 해당 루트 노드의 값을 읽는 순회이다.
왼쪽 링크를 통한 왼쪽 서브 트리 방문 -> 오른쪽 링크를 통한 오른쪽 서브 트리 방문 -> 서브 트리의 루트 방문(값 Get)

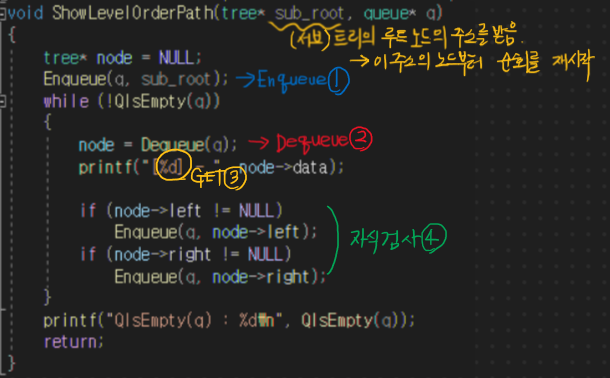
레벨 순회 : 레벨 순회는 레벨 1부터 트리의 말단 리프 노드들이 있는 레벨까지 큐 자료 구조에 순서대로 넣고 출력하여 순회하는 간단한 순회 법이며, 레벨 순서 & 왼 -> 오 순으로 순회가 이루어진다.
각 순회의 실제 결과

다음 포스팅은 이진 탐색 트리에서 탐색과 삭제 연산을 포스팅할 것이다.
'프로그래밍응용 > C 자료구조' 카테고리의 다른 글
| C Data Structure - 이진 탐색 트리 4 (마지막) (0) | 2021.01.24 |
|---|---|
| C Data Structure - 이진 탐색 트리 3 (0) | 2021.01.24 |
| C Data Structure - 이진 탐색 트리 1 (0) | 2021.01.23 |
| C Data Structure - 덱(디큐?) (0) | 2021.01.22 |
| C Data Structure - 리스트 기반 큐 (0) | 2021.01.20 |