그노므 DFS! DFS! 드디어 깔끔하게 정리를 한다. 이 탐색 기법 하나에 워낙 들어가는 내용이 많기 때문에 바로바로 정리하지 않으면 다시 처음부터 공부하는 수준으로 공부를 해야한다 흑흑...
이전의 포스팅의 내용을 기반으로 작성되기 때문에 이전 부분을 포스팅을 참고하라고 올려놓겠다.
C Data Structure - 그래프의 기본
드디어 그래프의 기본 코드이다. 이전 포스팅에서 설명했듯이, 그래프를 표현하는 방법 중 인접 리스트 방법을 이용하여 기본적인 그래프를 구현해 볼 것이다. 그 인접 리스트에 해당하는 방법
typingdog.tistory.com
C Data Structure - 땡땡 우선 탐색(Depth or Breadth First Search Graph)
C Data Structure - 그래프란? 드디어 그래프에 대한 포스팅이다. 여러가지 병행하며 정리할 것도 너무 많아서 ㅋㅋ 미루고 미루다 이제 올리게 된다. 오늘은 그래프의 기본 중에 기본인 용어 및 정의
typingdog.tistory.com
중요 핵심
일단은 깊이 우선 탐색은 아래 세 가지가 핵심이다.
1. 깊이 접근하는 것
2. 왔던 경로를 되돌아오는 것
3. 정점 방문 여부를 기록하는 것
이 세 가지를 핵심으로 기록하겠다. 사용되는 예시는 간단하게 다음과 같다.

첫 번째, 깊이 접근한다는 것은 한 정점에서 연결되어 있는 정점 중 하나의 정점을 선택해서 파고 들어가고 또 그 정점에서 연결된 정점 중 하나의 정점을 파고 들어가는 식의 방법을 이야기 한다.

1로 갈지, 2로 갈지는 중요하지 않다. 0이라는 정점에 연결 되어 있는 정점이 1 먼저 연결되있는지, 2 먼저 연결 되어있는지에 따라 다르다. 즉, 정점의 연결 정보를 나타내는 연결 리스트의 정렬 구조에 따라서 1 노드와 2 노드 중 어떤 것을 선택하게 될지 결정된다는 소리이다. 어찌됐건 우리는 순회 하는 것이 목적이므로 어딜 먼저 방문하는지는 의미가 없다.
두 번째, 왔던 경로를 되돌아오는 것은 되돌아오면서 놓친 정점을 순회해야하는 것이다. 이 때 경로를 다시 되돌아오려면 경로를 일단 기록을 해야하는데 역행이므로 스택의 형식대로 기록하면 된다. -> 방문 추적을 목적으로 스택을 사용한다.

세 번째, 정점 방문 여부를 기록한다는 것은 일반 순차 배열을 이용하여 기록한다. 다음 그림에 설명을 포함시키겠다.

주요 3가지 핵심에 대해서 살펴보았고 이번엔 그 순서대로 그려볼 것이다...
순회 프로세스

시작 정점 0을 방문된 상태로 시작한다. -> 방문 Flag 배열에서 정점 0을 True 처리.
연결된 인접 정점은 1 정점과 2 정점인데 방문 Flag 배열을 봐도 방문 처리가 False이기 때문에 두 정점 모두 접근이 가능하다. 이 예에서는 2 정점을 방문하겠지만 1 정점으로 방문해도 순회 순서만 다를 뿐 다른 의미는 없다.
2 정점을 방문하면서 방문 Flag 배열에서 2 정점을 True(방문) 처리하고, 떠나온 0 정점은 다시 돌아가기 위한 발자국으로 남기기 위해서 스택에 넣는다.

위와 마찬가지 과정을 통해 2 정점을 떠나면서 스택에 2 정점을 넣고, 3 정점을 방문한 뒤 방문 Flag 배열의 3 정점에 대한 방문 여부를 True로 변경한다.

또 마찬가지로 같은 과정을 반복하는데 3 정점에서는 1 정점과 4 정점에 접근 가능하다 어디로 가든 상관없지만 이번 예에서는 4 정점에 방문할 것이다.

4 정점에서는 인접한 정점이 모두 방문 처리 되었으므로 이제 스택에서 값을 POP 함으로써 되돌아 가면서 그냥 지나친 정점을 탐색한다.
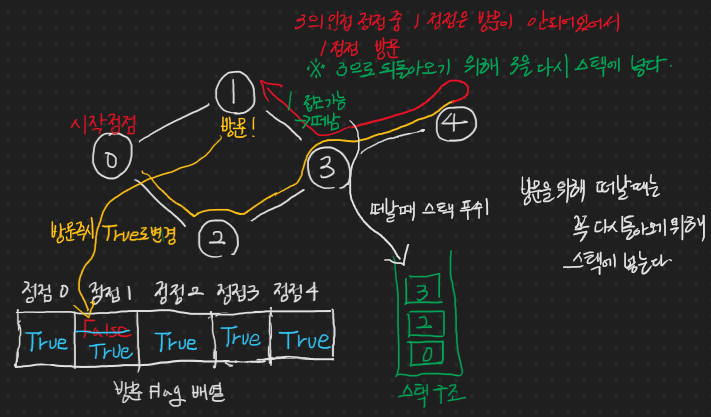
3 정점으로 돌아왔을 때, 보니까 1 정점을 방문하지 않고 그냥 지나쳤었기 때문에 1 정점에 방문한다. 이 때, 1 정점에 방문하기 위해서 3 정점을 떠나는 것이니 1 정점 방문 이후 다시 돌아오기 위해 3 정점을 다시 스택에 넣는다. 그리고 1 정점에 대한 방문 처리를 진행한다.

그리고 1 정점에서 인접 정점 모두 방문 처리 되었으니 Pop을 통해 돌아가고, 3 정점에서도, 2 정점에서도 마찬가지로 인접 정점 모두 방문처리 되었으므로 Pop을 통해 돌아가다가 0 시작 정점까지 Pop하여 스택이 빈 경우 비로소 모든 순회가 끝난 것이다.
0 -> 2 -> 3 -> 4 -> 1 순으로 순회가 이루어졌다.
진짜 뇌리에 박히겠다 박히겠어 정말 ㅋㅋ
이제 관련된 부분 코드를 보도록 하겠다.
코드 분석
스택이 새롭게 사용되므로 스택에 대한 코드가 필요한데 이미 만들어놓았던 배열 기반의 스택 코드를 활용할 것이다. 스택 설명 기록은 아래의 링크에서 확인하면 된다.
C Data Structure - 스택
스택이란 정말 간단하다. 분명히 내가 이거 그림 그리면서 포스팅을 한거 같은데 아무리 블로그를 뒤져봐도 없다... 그래서 다시 하는 느낌으로 스택 첫 포스팅을 시작한다. 먼저, 스택이란 무엇
typingdog.tistory.com
먼저 바뀌는 부분과 추가되는 부분이다.
그래프 내의 방문 Flag 배열이 추가 된다.

방문 처리를 수행하는 함수가 추가된다.
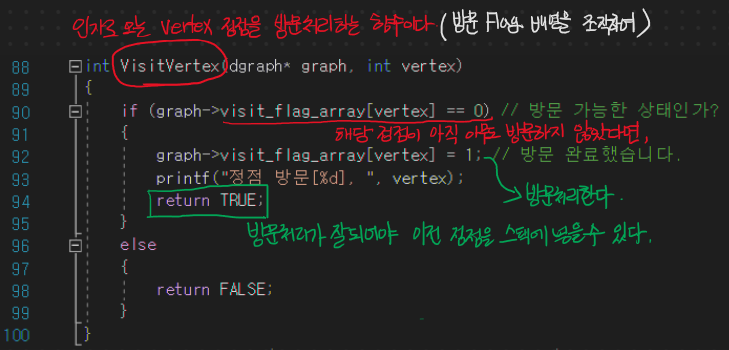
깊이 우선 탐색을 수행하는 함수이다.

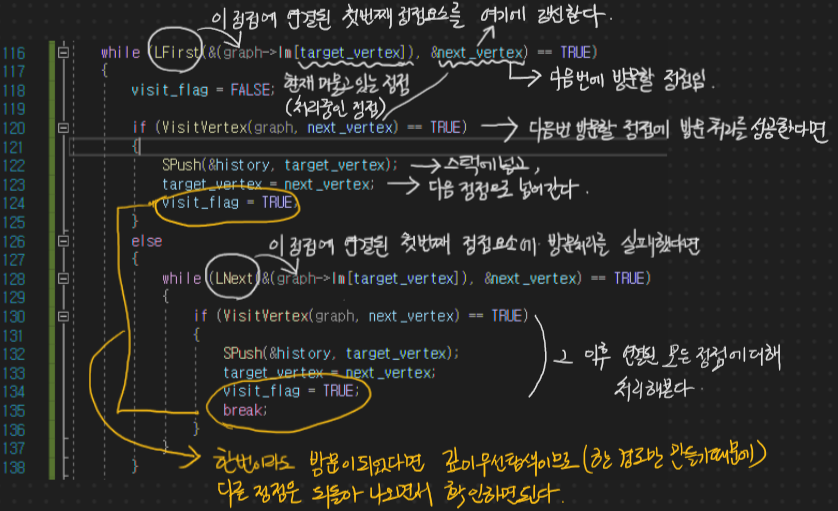
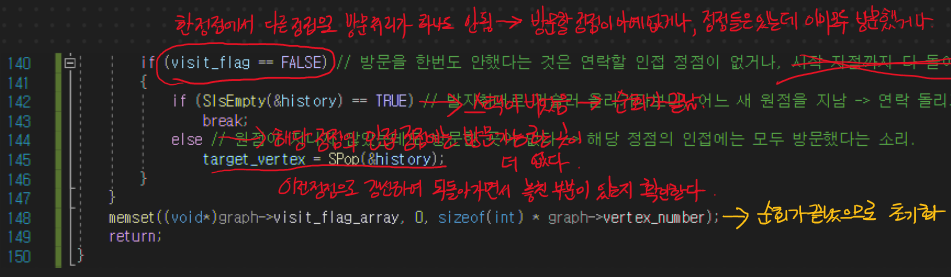
한 함수이지만 라인 수를 맞춰서 읽으면 된다... 이전 자료구조인 스택에 대한 사용 방법 또한 익혀야 하고 너무나도 추상적이라서 용어 설명이 너무 어려운 것 같다..ㅠ.ㅠ
그래프 종료 및 메모리 공간 해체 관련 코드이다.

전체 코드 및 실행 결과
전체 코드는 배열 기반의 스택과 변형된 연결리스트(오름차순으로 노드를 삽입; 이전에는 그냥 삽입했다.), DFS로 인해 변경된 그래프 코드 순으로 업로드 한다.
배열 기반의 스택 ArrayBasedStack.h -- -- -- -- --
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
/*
게시 완료
*/
#include <stdio.h>
#define STACK_LEN 10
#define TRUE 1
#define FALSE 0
struct array_stack
{
int stack_arr[STACK_LEN];
int top_index;
};
typedef array_stack stack;
void StackInit(stack* s);
int SIsEmpty(stack* s);
void SPush(stack* s, int data);
int SPop(stack* s);
int SPeek(stack* s);
void StackInit(stack* s)
{
s->top_index = -1;
return;
}
int SIsEmpty(stack* s)
{
if (s->top_index == -1) // 같아도 된다고?
return TRUE;
else
return FALSE;
}
void SPush(stack* s, int data)
{
if (s->top_index == STACK_LEN)
{
//printf("스택이 꽉 찼습니다.\n");
return;
}
s->stack_arr[++(s->top_index)] = data;
//printf("스택에 %d 값이 추가 되었습니다.\n", s->stack_arr[s->top_index]);
return;
}
int SPop(stack* s)
{
if (SIsEmpty(s))
{
//printf("스택이 이미 비어져 있습니다.\n");
return -1; // 적절치 않다. -1 또한 값으로 넣을 수 있기 때문에. -> 차라리 프로그램을 종료시키는게 적절.
}
return s->stack_arr[s->top_index--];
}
int SPeek(stack* s)
{
if (SIsEmpty(s))
{
//printf("스택이 텅 비었습니다.\n");
return -1;
}
return s->stack_arr[s->top_index];
}
|
cs |
변형된 연결 리스트 linkedlistforgraph.h -- -- -- -- --
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
|
#pragma once
#include <stdio.h>
#include <stdlib.h>
struct ListNode {
int data;
struct ListNode* link;
};
struct ListManager
{
struct ListNode* head;
struct ListNode* ci; // current index;
struct ListNode* pi; // previous index;
int (*comp)(int d1, int d2);
int node_count; // data 값이 유효한 node의 수
int malloc_count; // 할당된 수
};
void ListInit(struct ListManager* lm);
void LInsertNoSort(struct ListManager* lm, int data);
void FInsert(struct ListManager* lm, int data);
void SInsert(struct ListManager* lm, int data);
void LInsert(struct ListManager* lm, int data);
int LFirst(struct ListManager* lm, int* data);
int LNext(struct ListManager* lm, int* data);
int LCount(struct ListManager* lm);
int LRemove(struct ListManager* lm);
int WhoIsPrecede(int d1, int d2);
void SetSortRule(struct ListManager* lm, int (*comp)(int d1, int d2));
void* CreateNodeMemory(struct ListManager* lm, int len);
void ShowList(struct ListManager* lm);
void DeleteNode(struct ListManager* lm, struct ListNode* target);
void DeleteList(struct ListManager* lm);
void ListInit(struct ListManager* lm)
{
// count 초기화
lm->node_count = 0;
lm->malloc_count = 0;
// head 다음으로 항상 유지하는 빈 노드 생성
struct ListNode* new_node = (struct ListNode*)CreateNodeMemory(lm, sizeof(struct ListNode));
new_node->data = -1;
new_node->link = NULL; // 제일 끝이므로 무조건 NULL을 갖는다.
// 연결리스트 헤드 초기화
lm->head = (struct ListNode*)CreateNodeMemory(lm, sizeof(struct ListNode));
lm->head->data = -1;
lm->head->link = new_node;
// 인덱스 초기화
lm->ci = NULL;
lm->pi = NULL;
SetSortRule(lm, WhoIsPrecede);
//lm->comp = NULL;
return;
}
void LInsertNoSort(struct ListManager* lm, int data)
{
struct ListNode* new_node = (struct ListNode*)CreateNodeMemory(lm, sizeof(struct ListNode));
// head 다음의 빈 노드에 값을 반영, 링크는 건들지 않는다.
lm->head->link->data = data;
// empty_node 설정
new_node->data = -1;
new_node->link = lm->head->link;
lm->head->link = new_node;
lm->node_count++;
return;
}
void FInsert(struct ListManager* lm, int data)
{
struct ListNode* new_node = (struct ListNode*)CreateNodeMemory(lm, sizeof(struct ListNode));
// head 다음의 빈 노드에 값을 반영, 링크는 건들지 않는다.
lm->head->link->data = data;
// empty_node 설정
new_node->data = -1;
new_node->link = lm->head->link;
lm->head->link = new_node;
lm->node_count++;
return;
}
void SInsert(struct ListManager* lm, int data)
{
struct ListNode* new_node = (struct ListNode*)CreateNodeMemory(lm, sizeof(struct ListNode));
struct ListNode* pred = lm->head->link;
new_node->data = data;
while (pred->link != NULL && lm->comp(data, pred->link->data) != 0)
pred = pred->link;
// predecessor이 마지막 노드이면 그냥 거기다가 추가하면 되기 때문에 마지막 노드까지 가지 아니한다.
new_node->link = pred->link;
pred->link = new_node;
(lm->node_count)++;
return;
}
void LInsert(struct ListManager* lm, int data)
{
if (lm->comp == NULL)
{
printf("FInsert();\n");
FInsert(lm, data);
}
else
{
printf("SInsert();\n");
SInsert(lm, data);
}
return;
}
int LFirst(struct ListManager* lm, int* data)
{
if (lm->node_count == 0)
{
printf("순회할 노드가 없습니다.\n");
return false;
}
lm->ci = lm->head->link->link;
lm->pi = lm->head->link;
*data = lm->ci->data;
return true;
}
int LNext(struct ListManager* lm, int* data)
{
if (lm->ci->link == NULL)
return false;
lm->pi = lm->ci;
lm->ci = lm->ci->link;
*data = lm->ci->data;
return true;
}
int LCount(struct ListManager* lm)
{
return lm->node_count;
}
int LRemove(struct ListManager* lm)
{
int remove_value = lm->ci->data;
struct ListNode* rtarget = lm->ci;
lm->pi->link = rtarget->link;
lm->ci = lm->pi;
DeleteNode(lm, rtarget);
return remove_value;
}
int WhoIsPrecede(int d1, int d2)
{
if (d1 < d2)
return 0; // d1이 정렬 순서상 앞선다.
else
return 1; // d2가 정렬 순서상 앞서거나 같다.
}
void SetSortRule(struct ListManager* lm, int (*comp)(int d1, int d2))
{
lm->comp = comp;
return;
}
void* CreateNodeMemory(struct ListManager* lm, int len)
{
lm->malloc_count++;
return (void*)malloc(len);
}
void ShowList(struct ListManager* lm)
{
struct ListNode* index_node = NULL;
if (lm->malloc_count == 0)
{
printf("head와 new node 및 일반 node들까지 모두 존재하지 않습니다.");
return;
}
else if (lm->node_count == 0)
printf("추가된 노드는 모두 제거된 상태이지만, head와 new node가 존재하고 추가 가능한 상태입니다.\n");
for (index_node = lm->head; index_node != NULL; index_node = index_node->link)
{
printf("[%d|%p]", index_node->data, index_node);
if (index_node->link != NULL)
printf("->");
}
fputc('\n', stdout);
return;
}
void DeleteNode(struct ListManager* lm, struct ListNode* target)
{
if (target->data != -1)
lm->node_count--;
free(target);
lm->malloc_count--;
return;
}
void DeleteList(struct ListManager* lm)
{
struct ListNode* index_node = NULL;
struct ListNode* next_node = NULL;
for (index_node = lm->head; index_node != NULL; index_node = next_node)
{
next_node = index_node->link;
DeleteNode(lm, index_node);
}
if (lm->malloc_count != 0)
printf("메모리 해체에 문제가 있습니다\n");
return;
}
|
cs |
DFS로 인해 변경된 그래프 코드 DepthFirstSearchGraph.cpp -- -- -- -- --
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
|
#include <memory.h>
#include "NonPublishing/Graph/linkedlistforgraph.h"
#include "NonPublishing/Graph/ArrayBasedStack.h"
#define TRUE 1
#define FALSE 0
struct DefaultGraph
{
int vertex_number; // 정점의 수
int edge_number; // 간선의 수
struct ListManager* lm; // 정점 별 이어져 있는 간선들 관리.
int* visit_flag_array; // 정점에 방문했는지 안했는지 여부를 저장.
};
typedef struct DefaultGraph dgraph;
void GraphInit(dgraph* graph, int vertex_number);
void AddEdge(dgraph* graph, int from, int to);
void ShowGraphEdgeInfo(dgraph* graph);
void DestroyGraph(dgraph* graph);
int VisitVertex(dgraph* graph, int vertex);
void ShowDFSVertexes(dgraph* graph, int start_vertex);
int main(void)
{
dgraph graph;
GraphInit(&graph, 7);
//0 1 2 3 4
AddEdge(&graph, 0, 1);
AddEdge(&graph, 0, 3);
AddEdge(&graph, 1, 2);
AddEdge(&graph, 3, 2);
AddEdge(&graph, 3, 4);
AddEdge(&graph, 4, 5);
AddEdge(&graph, 4, 6);
ShowGraphEdgeInfo(&graph);
ShowDFSVertexes(&graph, 0); fputc('\n', stdout);
ShowDFSVertexes(&graph, 2); fputc('\n', stdout);
ShowDFSVertexes(&graph, 4); fputc('\n', stdout);
ShowDFSVertexes(&graph, 6); fputc('\n', stdout);
DestroyGraph(&graph);
return 0;
}
void GraphInit(dgraph* graph, int vertex_number)
{
int i = 0;
graph->vertex_number = vertex_number;
graph->edge_number = 0;
graph->lm = (ListManager*)malloc(sizeof(ListManager) * vertex_number);
graph->visit_flag_array = (int*)malloc(sizeof(int) * vertex_number); // 정점의 수만큼을 크기로 한다.
for (i = 0; i < vertex_number; i++)
ListInit(&(graph->lm[i]));
memset(graph->visit_flag_array, 0, sizeof(int) * vertex_number);
return;
}
void AddEdge(dgraph* graph, int from, int to)
{
if ((from >= graph->vertex_number) || (to >= graph->vertex_number))
{
printf("초과된 vertex 값이 왔습니다. \n");
return;
}
if (from == to)
{
printf("잘못된 vertex 값이 왔습니다. \n");
return;
}
LInsert(&(graph->lm[from]), to);
LInsert(&(graph->lm[to]), from);
graph->edge_number++;
return;
}
int VisitVertex(dgraph* graph, int vertex)
{
if (graph->visit_flag_array[vertex] == 0) // 방문 가능한 상태인가?
{
graph->visit_flag_array[vertex] = 1; // 방문 처리 했습니다.
printf("정점 방문[%d], ", vertex);
return TRUE;
}
else
{
return FALSE;
}
}
void ShowDFSVertexes(dgraph* graph, int start_vertex)
{
stack history;
int target_vertex = start_vertex;
int next_vertex;
int visit_flag = FALSE;
StackInit(&history);
// 시작 정점의 방문
if (VisitVertex(graph, target_vertex))
SPush(&history, target_vertex);
else
return;
while (LFirst(&(graph->lm[target_vertex]), &next_vertex) == TRUE)
{
visit_flag = FALSE;
if (VisitVertex(graph, next_vertex) == TRUE)
{
SPush(&history, target_vertex);
target_vertex = next_vertex;
visit_flag = TRUE;
}
else
{
while (LNext(&(graph->lm[target_vertex]), &next_vertex) == TRUE)
{
if (VisitVertex(graph, next_vertex) == TRUE)
{
SPush(&history, target_vertex);
target_vertex = next_vertex;
visit_flag = TRUE;
break;
}
}
}
if (visit_flag == FALSE)
{
if (SIsEmpty(&history) == TRUE)
break;
else
target_vertex = SPop(&history);
}
}
memset((void*)graph->visit_flag_array, 0, sizeof(int) * graph->vertex_number);
return;
}
void ShowGraphEdgeInfo(dgraph* graph)
{
int i = 0;
for (i = 0; i < graph->vertex_number; i++)
{
printf("정점[%d] : ", i);
ShowList(&(graph->lm[i]));
}
return;
}
void DestroyGraph(dgraph* graph)
{
int i = 0;
if (graph->lm == NULL)
return;
for (i = 0; i < graph->vertex_number; i++)
DeleteList(&(graph->lm[i])); // 내부 연결된 노드를 모두 제거.
free(graph->lm); // 정점들 자체를 제거.
free(graph->visit_flag_array); // 정점 방문 여부를 제거.
return;
}
|
cs |

'프로그래밍응용 > C 자료구조' 카테고리의 다른 글
| C Data Structure - 테이블 (0) | 2021.01.30 |
|---|---|
| C Data Structure - 너비 우선 탐색(Breadth First Search Graph) (0) | 2021.01.30 |
| C Data Structure - 땡땡 우선 탐색(Depth or Breadth First Search Graph) (0) | 2021.01.29 |
| C Data Structure - 그래프의 기본 (0) | 2021.01.28 |
| C Data Structure - 그래프란? (0) | 2021.01.28 |