미루고 미뤄왔던 보간 탐색에 대한 포스팅이다!!!
C Data Structure - 이진 탐색
이진 탐색을 구현해보았다. 이진 탐색에 대해 간단하게 기록하기 전에 이진 탐색의 전제 조건에 대해서 기록을 먼저 해보겠다. 이진 탐색의 전제 조건 이진 탐색은 오름차순이든 내림차순이든
typingdog.tistory.com
위에는 보간 탐색의 기반이 될 탐색의 원리를 설명해 놓은 글이다. 무려, 4개월 ~ 5개월 전에 내가 작성했던 글이다. 지금 봐도 상당히 디테일하게 잘 작성한 것 같은데 , 코드라던가 실행 결과 등을 제대로 올리지는 않았더라.
그래서 이번 포스팅에서 보간 탐색과 함께 이진 탐색의 재귀적 구현, 이진 탐색의 반복문 구현까지 원쁘라스투(1+2) 형태로 포스팅 들어간다.
먼저, 보간 탐색이 Main 이니 보간 탐색에 대해 살펴보도록 한다.
보간 탐색이란?
이진 탐색을 살짝 더 효율적으로 개선한 것이다! 기존의 이진 탐색의 경우 다음과 같이 탐색이 진행되는데,
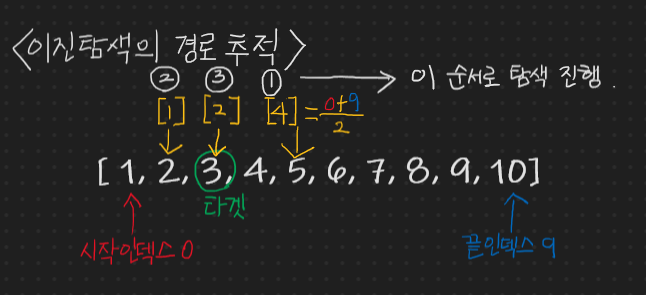
3번의 이진 탐색이 진행되었고, 그 3번의 이진 탐색 안에는 수 많은 계산들과... 수 많은 조건 검사 등으로 인해 그냥 선형 순차 탐색만도 못한 효율이 나와버렸다. 그 이진 탐색 시켜주려고 정렬까지 한 것을 생각해보면 억울하다.
물론.. 미미한 성능 차이이고, 데이터가 더 많고, 타겟이 더 안쪽에 있었을 때에는 분명히 이진탐색이 개쩔긴하다ㅋㅋ 예를 들기 위해서 극단적으로 말해본 것이다.
왜 위와 같이 선형 순차 탐색보다도 못한 결과가 일어났을까? 왜냐하면...
첫 번째, 데이터가 생각보다 앞에 있었기 때문이다.
두 번째, 죽으나 사나 수행하는 반 절 나누기로 인해서 절반 지점부터 시작하는 탐색 시작 위치가 문제이다.
그래서 데이터가 극 초반이나, 극 후반에 존재할 경우에도 계속 반절부터 시작할꺼냐! 라는 생각에서부터 시작되었다.
첫 번째 원인은 타겟이 치우져 있는 것은 우리가 어떻게 할 수 없는 것이다. 사용자가 찾겠다고 하는 타겟이 거기 있는걸 무슨 수로 해결하는가?
그렇다면 두 번째, 앞으로 절반 지점부터 시작하지 않으면 되지않을까?

그래서 이렇게 바꿔봤다. 이 공식은 아마도 수학 센세들이 힘들게 연구한 공식이 아닐까 한다. 저 공식은
"내가 찾는 값과 그 값이 저장되어 있는 위치는 비례하기 때문에 전체 길이에서
대충 이 정도 어디쯤에느으으은~~ 있지 않겠는가?"
를 이야기하는 공식이다. 그럴 수 밖에 없는게 이진 탐색과 마찬가지로 정렬되어 있는 데이터 세트를 대상으로 하기 때문에 당연히 전체 길이에서 찾으려는 값은 어림잡아 이쯤에 있겠거니 하고 추측해볼 수 있는 것이지 않겠는가?
그래서 그걸 실제로 구현해 본 예이다.

그런데 다음과 같은 예에서 탈출 조건에 문제가 있다.

위의 조건대로 데이터 세트와 타겟을 2로 조정하여 실행해보면 실행이 무한 루프에 빠진다. 즉, 탈출 해야하는데 탈출 조건을 충족시키지 못해서 무한 루프에 빠지는 것이다.
그렇다면 왜 이전 탈출 조건인 start <= end 조건은 먹히지 않는걸까? 그 이유를 아래에 정리해 보았다.

그도 그럴 것이, 새로 정의된 공식으로 인해서 정해지는 index 값은 "너가 찾는 타겟 값은 전체 길이 중에 대충 어디어디 쯤에 있어~" 라고 이야기해주는 것과 같다. 그렇다보니, 아무리 start 와 end 가 갱신된다고 하더라도 이전과 비슷한 index 값을 계산해서 내놓을 확률이 높다. 더군다나 start가 1밖에 증가하지 않은(범위가 겨우 인덱스 하나 줄어든) 상황에서는 더더욱 그럴 확률이 높다. 이런 와중에 갱신된 범위가 target이 포함되지 않는 상황까지 되어버린 것이다. 그러면 아주 그냥 삼위일체이다.
위의 예시 상황으로 보자면 다음과 같은 입장들이 되는 것이다.
새 공식 曰 : target 2는 인덱스 0 쯤에 있어~, index = 0 ~
start, end 曰 : 오 마침 index가 0이고 index+1이 start로 넘어오니 결국, 범위가 하나 밖에 안 줄었네?
arr[start], arr[end] 曰 : 3 ~ 9 값이군.
target 曰 : 난 2인데!!!! 왜 3 ~ 9를 보고 있냐!!! 다음 재귀 호출 때 탈출해라!!!
[ 재귀 호출 ]
탈출 조건 曰 : 응~ start <= end 조건 성립해서 탈출 안 해 ~
새 공식 曰 : (범위가 하나 줄은 것 가지고는 결과는 그대로겠네..?) 음.. 뭐.. target 2는 인덱스 0쯤에 있어~, index = 0 ~
[... 무한 반복 ...]
컴파일러 曰 : '신발장 크레파스 놈들이!!!!!!!!!!!!!!!!!!!!! 꽥(무한 루프 터.짐.)'
위의 대화가 탈출 조건과 새 공식의 순서가 코드와 조금 다르긴 하지만 문제는 없다. 결국은 같기 때문이다.
뭐 위 대화까지 보고도 이해가 안된다면 내 잘못이다. 설명을 못한 것이다. 근데 이게 글로만 설명하기 겁나 애매하고 짜증난다 ㅋㅋㅋㅋㅋㅋㅋㅋㅋ
아래는 코드와 실행결과이다. 탈출 조건까지 최종 수정된 보간 탐색과 이진 탐색의 재귀적 구현과 반복적 구현까지 모두 넣어 놓은 3종 세트인 것이다.
코드와 실행 결과
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
|
#include <stdio.h>
// 이진 탐색 반복적 구현
int BinarySearch(int arr[], int len, int target)
{
int begin = 0, end = len - 1;
int mid = -1;
while (begin <= end)
{
mid = (begin + end) / 2;
printf("반복! [mid = %d]\n", mid);
if (arr[mid] == target)
return mid;
else
{
if (target > arr[mid])
begin = mid + 1;
else
end = mid - 1;
}
}
return -1;
}
// 이진 탐색 재귀적 구현
int BinarySearchRecursive(int* arr, int begin, int end, int target)
{
int mid = (begin + end) / 2;
printf("재귀 함수 호출! [mid = %d]\n", mid);
if (begin <= end)
{
if (target == arr[mid])
return mid;
else if (target > arr[mid])
return BinarySearchRecursive(arr, mid + 1, end, target);
else if (target < arr[mid])
return BinarySearchRecursive(arr, begin, mid - 1, target);
}
else
return -1;
}
// 보간 탐색 재귀적 구현
int InterpolationSearchRecursive(int* arr, int start, int end, int target)
{
int index = ((double)(target - arr[start]) / (arr[end] - arr[start]) * (end - start)) + start;
printf("보간 재귀 함수 호출! [index = %d]\n", index);
if (arr[start] <= target && arr[end] >= target) // if (start <= end)
{
if (target == arr[index])
return index;
else if (target > arr[index])
return InterpolationSearchRecursive(arr, index + 1, end, target);
else if (target < arr[index])
return InterpolationSearchRecursive(arr, start, index - 1, target);
}
else
return -1;
}
int main(void)
{
int arr[] = { 1, 3, 5, 7, 9 };
int target = 2;
int result = -1;
// 보간 탐색 재귀적 구현 호출
printf("\n\n보간 탐색 재귀적 구현 호출 - - - - - - - - - - - - \n");
result = InterpolationSearchRecursive(arr, 0, sizeof(arr) / sizeof(int) - 1, target);
if (result != -1)
{
printf("[interpolation recursive] [%d는 arr배열의 %d 번째 위치에 존재합니다\n", target, result);
}
else
{
printf("[interpolation recursive] %d는 arr 배열에 존재하지 않습니다.\n", target);
}
// 이진 탐색 재귀적 구현 호출
printf("\n\n이진 탐색 재귀적 구현 호출 - - - - - - - - - - - - \n");
result = BinarySearchRecursive(arr, 0, sizeof(arr) / sizeof(int) - 1, target);
if (result != -1)
{
printf("[recursive] [%d는 arr배열의 %d 번째 위치에 존재합니다\n", target, result);
}
else
{
printf("[recursive] %d는 arr 배열에 존재하지 않습니다.\n", target);
}
// 이진 탐색 반복적 구현 호출
printf("\n\n이진 탐색 반복적 구현 호출 - - - - - - - - - - - - \n");
result = BinarySearch(arr, sizeof(arr) / sizeof(int), target);
if (result != -1)
{
printf("[iteration] %d는 arr배열의 %d 번째 위치에 존재합니다\n", target, result);
}
else
{
printf("[iteration] %d는 arr 배열에 존재하지 않습니다.\n", target);
}
return 0;
}
|
cs |
없는 값으로 인해 탐색 실패 결과

탐색 성공

'프로그래밍응용 > C 자료구조' 카테고리의 다른 글
| C Data Structure - 기수 정렬 (0) | 2021.01.31 |
|---|---|
| C Data Structure - 해시 테이블 (0) | 2021.01.30 |
| C Data Structure - 테이블 (0) | 2021.01.30 |
| C Data Structure - 너비 우선 탐색(Breadth First Search Graph) (0) | 2021.01.30 |
| C Data Structure - 깊이 우선 탐색(Depth First Search Graph) (0) | 2021.01.29 |