#include <stdio.h>
#include <stdlib.h>
#define TRUE 1
#define FALSE 0
#define STACK_LEN 20
#define QUEUE_LEN 20
struct binary_tree_node
{
int data;
struct binary_tree_node* left;
struct binary_tree_node* right;
};
typedef struct binary_tree_node tree;
/////////////////////////////////////////////////////////////////////////////////////////////////////////////
// 스택으로 메모리 관리.
struct array_stack
{
struct binary_tree_node* stack_array[STACK_LEN];
int top_index;
};
typedef array_stack stack;
// 배열 기반 원형 큐 -> 레벨 순회를 위해서;
struct array_queue
{
int front;
int rear;
struct binary_tree_node* queue_array[QUEUE_LEN];
int count;
};
typedef struct array_queue queue;
/* 스택 함수 모음 */
void StackInit(stack* s);
int SIsEmpty(stack* s);
int SIsFull(stack* s); // 증가시키고 대입이기 때문에 현 index에서 증가시키고 대입이 가능한지를 확인해야함.
void SPush(stack* s, struct node* data); // 증가시키고 대입.
struct binary_tree_node* SPop(stack* s);
struct binary_tree_node* SPeek(stack* s);
void ShowStack(stack* s);
struct binary_tree_node* CreateNodeAuto(stack* s);
void RemoveAllNodeAuto(stack* s);
/* 큐 함수 모음 */
void QueueInit(queue* q);
int QIsEmpty(queue* s);
tree* Dequeue(queue* q);
tree* Enqueue(queue* q, tree* data);
void ShowQueue(queue* q);
/////////////////////////////////////////////////////////////////////////////////////////////////////////////
// 트리 관련 함수
// 생성 및 삽입
tree* AutoCreateBinaryTreeNode(tree* r, stack* s, int data)
{
// 조회를 위한 포인터 생성
tree* index = r;
// 새로운 노드 생성
tree* newnode = CreateNodeAuto(s);
// 새로운 노드 초기화
newnode->data = data;
newnode->left = NULL;
newnode->right = NULL;
// 순회 index가 NULL이 될 때까지 계속 돌린다.
if (index == NULL)
return newnode;
else
{
while (index != NULL) // TRUE
{
if (data < index->data)
{
if (index->left == NULL)
{
index->left = newnode; // 니가 있어야 할 곳은 여기야.
break;
}
// 현재 노드의 자식 중 left node로 간다.
else
{
index = index->left;
}
}
else if (data > index->data)
{
if (index->right == NULL)
{
index->right = newnode; // 니가 있어야 할 곳은 여기야.
break;
}
else
{
index = index->right;
}
}
}
return r;
}
}
// 전체 순회(전위, 중위, 후위)
void ShowPreOrderPath(tree* sub_root)
{
if (sub_root != NULL)
{
printf("[%d] - ", sub_root->data);
ShowPreOrderPath(sub_root->left);
ShowPreOrderPath(sub_root->right);
}
return;
}
void ShowInOrderPath(tree* sub_root)
{
if (sub_root != NULL)
{
ShowInOrderPath(sub_root->left);
printf("[%d] - ", sub_root->data);
ShowInOrderPath(sub_root->right);
}
return;
}
void ShowPostOrderPath(tree* sub_root)
{
if (sub_root != NULL)
{
ShowPostOrderPath(sub_root->left);
ShowPostOrderPath(sub_root->right);
printf("[%d] - ", sub_root->data);
}
return;
}
void ShowLevelOrderPath(tree* sub_root, queue* q)
{
tree* node = NULL;
Enqueue(q, sub_root);
while (!QIsEmpty(q))
{
node = Dequeue(q);
printf("[%d] - ", node->data);
if (node->left != NULL)
Enqueue(q, node->left);
if (node->right != NULL)
Enqueue(q, node->right);
}
printf("QIsEmpty(q) : %d\n", QIsEmpty(q));
return;
}
// 탐색
tree* SearchNode(tree* sub_root, int search_data)
{
if (sub_root == NULL)
return NULL;
else if (search_data == sub_root->data)
return sub_root;
else if (search_data < sub_root->data)
return SearchNode(sub_root->left, search_data);
else if (search_data >= sub_root->data)
return SearchNode(sub_root->right, search_data);
}
// 삭제
void RemoveNode(tree** root, int search_data)
{
tree* target = NULL, * target_parent = NULL;
tree* succ = NULL, * succ_parent = NULL;
// 타겟 탐색
target = *root;
while (target != NULL)
{
if (target->data == search_data)
{
break;
}
else if (search_data < target->data)
{
target_parent = target;
target = target->left;
}
else if (search_data > target->data)
{
target_parent = target;
target = target->right;
}
}
// 타겟의 유형 파악
if (target->left == NULL && target->right == NULL) // 타겟이 leaf node인 경우
{
if (target_parent == NULL && target == *root) // 노드가 루트 하나만 달랑 있는 경우
*root = NULL;
else if (target == target_parent->left)
target_parent->left = NULL;
else if (target == target_parent->right)
target_parent->right = NULL;
}
else if (target->left == NULL || target->right == NULL)
{
if (target_parent == NULL && target == *root)
*root = (target->left != NULL) ? target->left : target->right;
else if (target == target_parent->left)
target_parent->left = (target->left != NULL) ? target->left : target->right;
else if (target == target_parent->right)
target_parent->right = (target->left != NULL) ? target->left : target->right;
}
else if (target->left != NULL && target->right != NULL)
{
succ = target->right, succ_parent = target;
while (succ->left != NULL)
{
succ_parent = succ;
succ = succ->left;
}
target->data = succ->data;
if (succ_parent->left == succ)
succ_parent->left = succ->right;
else if (succ_parent->right == succ)
succ_parent->right = succ->right;
}
return;
}
int main(void)
{
tree* root = NULL;
tree* target = NULL;
stack s;
queue q;
StackInit(&s);
QueueInit(&q);
//삽입
/*root = AutoCreateBinaryTreeNode(root, &s, 15);
root = AutoCreateBinaryTreeNode(root, &s, 7);
root = AutoCreateBinaryTreeNode(root, &s, 20);
root = AutoCreateBinaryTreeNode(root, &s, 3);
root = AutoCreateBinaryTreeNode(root, &s, 10);
root = AutoCreateBinaryTreeNode(root, &s, 17);
root = AutoCreateBinaryTreeNode(root, &s, 27);
root = AutoCreateBinaryTreeNode(root, &s, 1);
root = AutoCreateBinaryTreeNode(root, &s, 2);
root = AutoCreateBinaryTreeNode(root, &s, 9);
root = AutoCreateBinaryTreeNode(root, &s, 13);*/
root = AutoCreateBinaryTreeNode(root, &s, 10);
root = AutoCreateBinaryTreeNode(root, &s, 4);
root = AutoCreateBinaryTreeNode(root, &s, 12);
root = AutoCreateBinaryTreeNode(root, &s, 2);
root = AutoCreateBinaryTreeNode(root, &s, 5);
root = AutoCreateBinaryTreeNode(root, &s, 20);
// 전위 순회
ShowPreOrderPath(root);
fputc('\n', stdout);
// 중위 순회
ShowInOrderPath(root);
fputc('\n', stdout);
// 후위 순회
ShowPostOrderPath(root);
fputc('\n', stdout);
// 레벨 순회
ShowLevelOrderPath(root, &q);
fputc('\n', stdout);
// 4와 12를 각각 탐색
target = SearchNode(root, 4);
if (target != NULL)
printf("%p 주소에서 %d 값을 찾았습니다.\n", target, target->data);
else
printf("해당 값이 트리에 존재하지 않습니다\n");
target = SearchNode(root, 12);
if (target != NULL)
printf("%p 주소에서 %d 값을 찾았습니다.\n", target, target->data);
else
printf("해당 값이 트리에 존재하지 않습니다\n");
// 노드 삭제
RemoveNode(&root, 10);
// 레벨 순회
ShowLevelOrderPath(root, &q);
fputc('\n', stdout);
// 메모리 관리
RemoveAllNodeAuto(&s);
return 0;
}
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// 메모리 관리 스택 관련 함수 모음
void StackInit(stack* s)
{
int i = 0;
s->top_index = -1;
for (i = 0; i < STACK_LEN; i++) // 순회를 위해서 모두 초기화
s->stack_array[i] = NULL;
return;
}
int SIsEmpty(stack* s)
{
if (s->top_index == -1)
return TRUE;
else
return FALSE;
}
int SIsFull(stack* s) // 증가시키고 대입이기 때문에 현 index에서 증가시키고 대입이 가능한지를 확인해야함.
{
if ((s->top_index) + 1 < STACK_LEN)
return FALSE;
else
return TRUE;
}
void SPush(stack* s, struct binary_tree_node* data) // 증가시키고 대입임 (top_index가 -1부터 시작하기 때문에)
{
if (SIsFull(s))
{
printf("스택이 가득찼습니다\n");
return;
}
s->stack_array[++(s->top_index)] = data;
return;
}
struct binary_tree_node* SPop(stack* s)
{
struct binary_tree_node* rtarget = NULL;
if (SIsEmpty(s))
{
printf("스택이 비어져있습니다\n");
return NULL;
}
rtarget = s->stack_array[s->top_index];
s->stack_array[s->top_index--] = NULL;
return rtarget;
}
struct binary_tree_node* SPeek(stack* s)
{
if (SIsEmpty(s))
{
printf("스택이 비어져있습니다\n");
return NULL;
}
return s->stack_array[s->top_index];
}
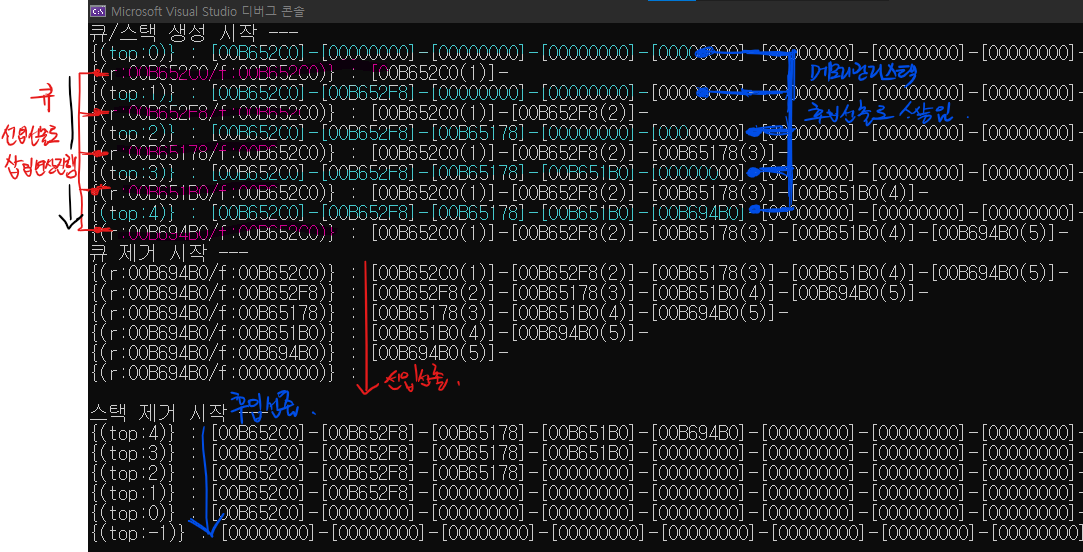
void ShowStack(stack* s)
{
int i = 0;
printf("{(top:%d)} : ", s->top_index);
for (i = 0; i <= s->top_index; i++)
printf("[%p](%d)", s->stack_array[i], s->stack_array[i]->data), putc('-', stdout);
putc('\n', stdout);
return;
}
binary_tree_node* CreateNodeAuto(stack* s)
{
struct binary_tree_node* tmp = (struct binary_tree_node*)malloc(sizeof(struct binary_tree_node));
// 초기화
tmp->data = 0;
tmp->left = NULL;
tmp->right = NULL;
// 메모리 스택에 추가
SPush(s, tmp);
return tmp;
}
void RemoveAllNodeAuto(stack* s)
{
binary_tree_node* rtarget = NULL;
ShowStack(s);
while (!SIsEmpty(s))
{
rtarget = SPop(s);
free(rtarget);
ShowStack(s);
}
return;
}
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
// 큐 함수 모음
void QueueInit(queue* q)
{
int i = 0;
q->front = q->rear = 0;
for (i = 0; i < QUEUE_LEN; i++)
q->queue_array[i] = NULL; // 큐 출력을 위한 초기화
q->count = 0;
return;
}
int QIsEmpty(queue* q)
{
if (q->front == q->rear)
return true;
else
return false;
}
tree* Dequeue(queue* q)
{
tree* rval = NULL;
// 기본 동작 - 비었는가 확인 -> 삭제 -> 인덱스 변경
if (q->front == q->rear)
{
printf("Queue가 이미 비었습니다.\n");
return 0;
}
rval = q->queue_array[q->front];
q->queue_array[q->front] = NULL;
q->front = (q->front + 1) % QUEUE_LEN;
q->count--;
return rval;
}
tree* Enqueue(queue* q, tree* data)
{
tree* rval = NULL;
// 기본 동작 - 꽉 찼는가 확인 -> 삽입 -> 인덱스 변경
// 2.
if ((q->rear + 1) % QUEUE_LEN == q->front) // 가득 찬 경우,
{
printf("Queue가 가득 찼습니다.\n");
return 0;
}
// 1.
q->queue_array[q->rear] = data;
rval = q->queue_array[q->rear];
q->rear = (q->rear + 1) % QUEUE_LEN;
q->count++;
return rval;
}
void ShowQueue(queue* q)
{
int i = 0;
printf("{(r:%2d/f:%2d)} : ", q->rear, q->front);
for (i = 0; i < q->count; i++)
printf("[%p]", q->queue_array[i]), putc('-', stdout);
putc('\n', stdout);
return;
}