꿈 꾸는 누렁이

이전 글에서 비유를 통해서 Multiplexing이 뭔지 느껴 보았을 터이다.

그 멀티플렉싱 기반의 다중 처리 소켓 모델이 있는데, 이 소켓 모델을 이용해서 다중 접속에 대한 처리를 서버 하나로 처리할 것이고, 그 과정을 정리하는 블로깅이다. 

이런 상황에서 서버를 어떻게 코딩 해야? 멀티 플렉싱 모델을 적용할 수 있을지를 기록할 것이다. 여기서 우리는 select 라는 함수를 사용하는데 일반 함수를 띡

strtok( ... );

호출하는 것과는 차원이 다르게 알아둬야 할 배경이 많다. 내가 느끼기엔 ㅋㅋ (strtok 함수도 사용하기 까다로웠음)

일단 기본 컨셉을 다루기 전에 앞서, 리눅스 시스템에서의 파일 디스크립터라는 개념을 알아야 한다. 윈도우의 경우에는 핸들이라는 개념으로 사용되는데 거의 비슷한 개념이라고 생각하고 모델을 구현해도 무리가 없다.

File Descriptor(파일 디스크립터) : 직역해보면 '파일 설명자'이다. 조금만 다듬으면 파일 식별자 라고 생각하면 되는데, 파일을 생성할 때, 해당 파일에 주어지는 번호라고 생각하면 된다. 즉, 그 파일을 간단하게 지목할 수 있는 번호표와 같다. 그런데 리눅스에서는 생성되는 파일 뿐만 아니라, 생성되는 소켓에 대해서도 파일 취급을 하고, 파일 디스크립터를 할당한다. 다음과 같이 말이다.(0과 1과 2는 표준 입출력들에 대해 이미 예약되어 있다. - 순서대로 stdin, stdout, stderr)

근데 이걸 왜 알아야하냐? select 함수는 바로 이 파일 디스크립터를 잘 요리조리 볶아서 다중 접속 처리를 하기 때문이다. 윈도우도 마찬가지다. 파일 디스크립터에서 핸들을 다룬다라는 것 외에는 다를 바가 없다.

그러면 기본 컨셉을 조금 표현해 볼 것이다.

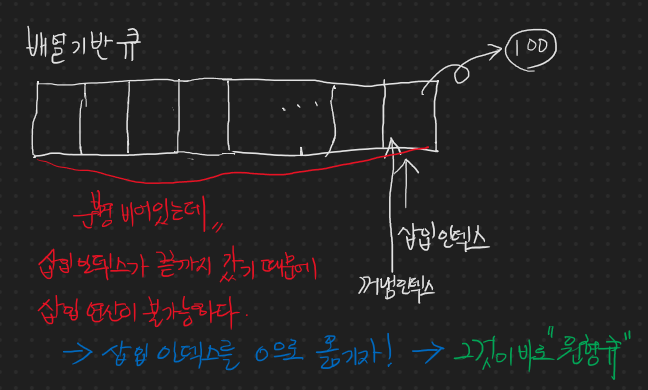
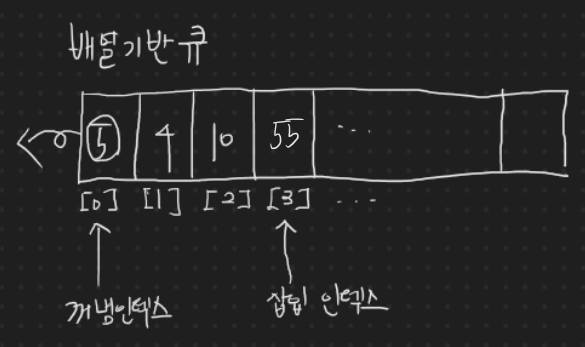
첫 번째, 파일 디스크립터의 등록이다.

그림 내의 글을 읽어보면 되지만, 부가 설명을 넣자면 fd_set 은 구조체 자료형이다. 

요런 식으루 생겼고 ㅋㅋ (답없다ㅋㅋ), 비트처럼 동작한다고 생각하면 된다. 생성된 소켓들의 파일 디스크립터들이 배열로 나열되고, 0과 1로 변화의 유무를 표현한다고 생각하면 마음이 편할 것 같다.ㅋㅋ

이러한 배열을 조작하는 매크로 함수가 위위 그림에 나열한 것들이다.

FD_ZERO : 해당 배열을 모두 0으로 초기화.
FD_SET : 해당 파일 디스크립터를 배열에 등록.
FE_CLR : 해당 파일 디스크립터를 배열에서 제거.
FD_ISSET : 해당 파일 디스크립터가 배열에 등록되어 있니? 

코드로 확인하겠다 나중에ㅋㅋ

두 번째, 준비는 완료 되었다! Select 함수의 호출이다!!!!

위에는 select 함수의 인자 설명이고, 아래는 호출의 예이다.

__nfds 인자는 select 함수가 검사할 파일 디스크립터의 범위를 묻는 것이다. 범위면 범위지 왜 max + 1 같은 숫자를 입력하는건가? 

리눅스에서 파일 디스크립터는 0부터 순차적으로 생성이 된다. 그러니까 제일 마지막에 생성되는 파일 디스크립터가 곧  총 생성된 파일 디스크립터 중 마지막 번호를 가지고 있을 것이고, 거기서 더하기 1을 한 값이 총 갯수가 된다. 

파일 디스크립터가 "순차적"으로 값이 증가하는 것이 보장되기 때문에 범위를 지정하는 항목에 끝 번호 + 1 이 올 수 있는거다. 끝 번호 + 1 을 알면 0 ~ 끝 번호가 범위겠거니~ 하면 되니까!

추가 -- 

아, 맞다! 윈도우 같은 경우는 핸들이 순차적으로 생성되지 않는다! 그래서 fd_set을 다루는 방법이 조금 다르긴 하다 ㅋㅋ 그래서 윈도우에서는 첫 번째 인자를 사용하지 않고 뭐 알아서 범위를 잡아서 계산해주나보다. 다만, 리눅스 소켓 계열과 호환성 때문에 남겨두었다고 한다. 이거 빼먹을 뻔 했음 - 근데 나는 리눅스 계열 소켓만 준비했기 때문에...

--

세 번째, select 함수 호출 이후 변화를 살펴볼 것이다. select 함수 호출 직 후부터 지정한 시간동안 변화가 발생했을 때와 발생하지 않았을 때를 본다.

시간을 지정한다고 했는데 간단하다. 아래 그림 두 장과 설명을 보면 된다.

먼저, 변화가 발생했을 때이다.

두 개 변화했으니 저 변한 녀석들에 대해서만 반복문이든 뭐든 써서 데이터 수신 처리와 그에 맞는 송신 처리를 진행하면 된다!! 참 쉽지 않는가!!!! 

저 두 녀석을 찾는 방법은 FD_ISSET 이라는 매크로 함수를 이용하여 찾아낸다. 정확히는

fd_set 배열 내 일어난 변화가 클라이언트1 fd인가?
fd_set 배열 내 일어난 변화가 클라이언트2 fd인가?

라는 질문을 FD_ISSET 과 조건문으로 주구장창 물어보면 된다 ㅋㅋ 그 방법은 코드로 익히는게 빠르다.

그럼 변화가 발생하지 않을 때에는? 

그냥 뭐 처리할게 없다. 왜냐? 뭔가 송신한 클라이언트가 없으니 변화가 안 일어났기 때문이다 ㅋㅋ

자, 이렇게 하면 과정들을 대충 훑어보았다. 개념만 대충 잡히면 된다. 나머지는 코드로 확실히 보면 되니까 말이다. 함수들이나 매개변수의 정확한 용어나 쓰임을 분석 단위로 보려면 찾아보면 된다. 그거 올려놓으면 나중에 까먹어서 다시 볼 때 하나도 머리에 안 들어오고 안 읽힌다 

다음 시간에는 코드다. 정리하기 너무 힘들다 진짜 ㅋ

최근, 아니 비교적 최근에 어떤 게임 클라이언트를 활용한 게임 서버를 만드는 프로젝트를 진행했던 적이 있고, 지금도 조금씩 조금씩 하고 있으나, 우선 순위에 밀려 소홀하긴 하지만 진행하고 있다. 

아무래도 게임 서버인 만큼 소켓 프로그래밍이 빠질 수가 없는 영역인데, 이를 개발하면 바로바로 기록해뒀어야 하는데 그러지 못해 지금 땅을 치고 후회하고 있다 휴...

그 프로젝트에서 사용된 소켓 모델은 I/O Multiplexing이다. 원래 처음에는 Multi Processing 기반으로 구현해보고, 한 100명 접속할 미래를 김칫국 마시 듯 생각해서 Multi Threading 기법으로 간단히 구현했다가, 신경써야 할 부분이 많아서 Multi plexing 기반으로 구현을 해보았다.

먼저 각각의 차이를 알아야 하는데, Thread 개념은 Processing 포스팅 때 비교하도록하고, 지금은 완전 다른 양상을 보이는 Plexing과 Processing을 비교하도록 하겠다.

나만의 비유가 들어간다.

A라는 과목을 가리치는 교사들이 있다. 이 클래스에는 A 과목만 들으러 학생들이 온다. 이는 전제이다.

멀티 프로세싱 모델을 비교한 것이다. 학생에게 마치 과외 선생님처럼 교사가 할당되어, 학생에게서 질문이나 요구를 받아서 그에 따른 대답을 해준다.

하지만 이는 매~우 비효율적이다. 전제처럼 같은 수업 내용을 듣는 학생들인데 교사가 굳이 일대 일로 붙는다는 것은 교사라는 재능, 인적 자원이 너무나도 낭비되는 것이다! 왜냐? 같은 과목을 듣는 학생을 한데 모아서, 질문이 있는 사람들에게만 대답해주고, 가르치는 것은 일방적으로, 기본적으로 수행하면 되기 때문이다! 

그래서 또 그려왔다.

얼마나 효율적인가, 학생들 입장에서는 특화된 교육을 못 받아서 질이 떨어졌다고 생각할 수 있지만 정말 실력이 좋은 교사로 채용할수록 교육의 질을 확실하게 커버할 수 있다.

바로 이 비유에서 볼 수 있듯이 여러 학생들에게 교사 한 명이 배치되어 '가르침'이라는 기본 동작을 수행하고, 질문을 하는 학생들을 대상으로 따로 처리를 한다.

이번에 기록하는 모델 또한 마찬가지이다.

여러 학생들에게 -> 접속해 온 여러 클라이언트들에게
교사 한 명 -> 서버 하나
기본 동작을 수행 -> 접속 요청 수락 및 접속 종료 등
질문을 하는 학생들 -> 패킷을 송신하는 클라이언트

접속해 온 여러 클라이언트들에게 서버 하나가 배치되어 '접속 요청 수락 및 접속 종료 등의 송 수신'이라는 기본 동작을 수행하고, 패킷을 송신하는 클라이언트들을 대상으로 따로 처리를 한다.

이렇게 바꿔서 서버-클라이언트 관점에서 이야기해볼 수 있다. 100% 기술적으로 맞지 않을 수 있지만 크게 보았을 때 그렇다는 것이다.

나는 그래서 앞으로 저 두 번째 그림에서의 교사에 대한 설명을 기록하고 만들 것이다! ㅋㅋ

드디어 원형 큐이다. 자기소개 페이지를 좀 작성하느라, 기록을 하지 못했다.. ㅎㅎ ㅠ.ㅠ

일단, 원형 큐이다. 지난 포스팅 기록에서 처럼 구조로 인해 어쩔 수 없는 단점과 문제를 가지고 있는 일반 배열 기반 큐에서 개선된 것이 원형 큐이다. 그 단점이자 문제는 다음과 같다.

아니 그러면, 삽입 인덱스와 꺼냄 인덱스를 모두 초기화 시켜서 다시 앞으로 옮겨오면 되는 것 아닌가? 라는 생각이 들었었는데 이를 반박할 수 있는 사례가 또 나타난다....

바로 이 경우이다. 순서대로 읽으면 된다. 35와 43 값을 추가 후, 배열의 끝이기 때문에 가정했던대로 삽입 인덱스를 초기화 시켜서 다시 삽입하여 공간을 활용하려는 노력이 보이는 그림이다. 그럼 만약에 위 상황에서 데이터를 순회하려면 어떻게 해야하는가?

7 -> 11 -> 15 -> 35 -> 43 으로 순회를 해야할까? 아니다. 이렇게 되면 큐의 기본 원리에 제대로 위배된다. 35와 43이 먼저 나와야한다. 

위 상황에서 큐의 기본 원리를 지키며 데이터를 순회하기 위해서는
1) 꺼냄 인덱스부터 먼저 확인 후 값을 꺼낸 뒤,
2) 다시 꺼냄 인덱스를 초기화하여 인덱스 0부터 들어간 값을 꺼내며 인덱스를 증가시키고,
3) 삽입 인덱스와 접하는지를 확인한다.
-> 2, 3 을 반복한다.

나 같으면 위와 같은 짓, 안 하겠다. 원형 큐에 대해 당장 알아본다.

먼저, 왼쪽과 같은 일반 배열을 오른쪽처럼 가상으로 구부렸다고 생각하고 모든 기록을 전개할 것이다. 기본 세팅에 대해서 좀 더 설명하자면, 다음 그림과 같다.

일반 큐처럼 삽입 인덱스와 꺼냄 인덱스가 존재하며, 이름이 각각 그림과 같이 달라질 뿐이다. 그리고 각 인덱스는 대입 연산이나 삭제 연산이 진행된 후에 증가하는 형태를 기본으로 한다.

그럼 삽입과 삭제는 그림 한 장으로 설명이 가능할 것 같다.

그렇다면 삽입을 하려면 큐가 꽉 찾는지 확인해야하며, 삭제하려면 큐가 비어있는지 확인해야한다. 원형 큐의 문제가 바로 이것이기 때문에 중요하다!!!!

먼저, 다음 그림을 보면 문제가 뭔지 알 수 있다

큐가 모두 비었을 때와 가득 찼을 때의 인덱스들의 상태가 완전히 똑같다. 인덱스의 위치에 상관없이 front가 rear을 따라 잡았다는 소리는 삭제를 모두 완료했다고 볼 수 있다. 그러나, rear이 front를 따라 잡았다는 소리는 삽입을 모두 완료했다고 볼 수도 있기 때문이다. 아주 기가 막힙니다.

그래서 원형 큐를 삽입할 때, 큐의 길이 - 1 만큼만 삽입하도록 할 예정이다. 꽉 찬 상태와 텅 빈 상태는 그림과 같다.

이 약속들만 지킨다면 원형 큐를 구현하면서 기가 막힐 일은 없을 것이다.

코드 및 실행 결과

----

----

그날 그날 정리하고 올려야 한다.. 묵혀두면 이렇게 고생한다.

-

오늘은 큐에 대해서 기록할 것이다. 큐는 굉장히 중요한 자료구조이다.

큐란 무엇인가?

비유해보자면 선착순이다. 먼저 온 사람이 먼저 서비스를 받는 것!

이를 두고 선입선출의 개념이라고 한다. 그림과 같이 나타낸다.

위 그림에서 옆으로 눕혀진 원통은 배열이라고 생각하면 된다. 배열에서 큐를 구현할 때를 생각해보자.

단순 배열 기반 큐에서의 삽입

단순 배열 기반의 큐에서 삽입 연산을 하는 것은 어려울 것이 없다. 배열의 끝에 값을 추가하듯이 인덱스를 증가시켜가면서 값을 넣으면 된다. 다음과 같이 말이다.

큐를 만들기 나름이지만, 인덱스를 증가시킨 후 삽입하는 것으로 하겠다.

단순 배열 기반 큐에서의 값의 꺼냄(삭제)

그러면 큐의 자료 구조 원칙에 맞도록 먼저 들어온 값을 꺼내려거든 어떻게 해야하나? 이런 경우는 삽입을 위한 인덱스를 하나 두고 증가시키면서 삽입을 진행하고, 꺼내려는 인덱스를 하나 두고 꺼내는 연산을 할 때마다 증가 시키면 된다!

삭제 또한 인덱스를 증가시킨 후 값을 삭제하는 것으로 하겠다.

큐의 꽉참/비워짐 여부 확인

큐를 가지고 삽입 / 삭제 연산을 진행하기 위해서 선행되어야 하는 연산은 큐가 비워졌는지 꽉 찾는지를 확인하면 된다. 아래의 그림은 큐의 비워진 상태를 나타대기 위해서 삽입은 멈추고, 꺼내는 연산만 한 그림이다. 

큐에 값이 꽉 찼음을 확인하는 방법은 선형 큐에서는 다음과 같다.

이 경우이다. 삽입 인덱스가 끝까지 가서 삽입 후 증가를 해야하는데 증가를 하려는데 증가가 안된다. 왜냐하면 인덱스가 끝에 왔기 때문이다. 이 경우 우리는 꽉 찼음을 확인한다. 

배열 기반 큐의 문제

위의 기록한 큐에는 문제가 있다. 다음과 같다.

이는 구조의 문제이다. -> 배열 길이가 정해져있고 순환하지 않는 선형이기 때문에 

이로 인해서 등장하는 것이 원형 큐이다!

원형 큐를 구현하면 선형 큐의 모든 개념 + 선형 큐의 문제 해결이 들어가기 때문에 선형 큐를 따로 포스팅하고 원형 큐에서 구현까지 마무리 지을 것이다.

내가 퀵 정렬까지 공부할 줄은 몰랐(었)다. 역시 차근차근 해 놓는게 중요하다. 더불어 포스팅도 그 때 그 때 하지 않으면 이렇게 개 고생한다.

어찌됐건 오늘은 퀵 정렬이다.

나는 이게 퀵 정렬이 겁나 빨라서 퀵 정렬인가 했는데, 맞다. 겁나 빠른 퀵 정렬 한 번 기록해둔다.

퀵 정렬이란?

퀵 정렬은 이름을 통해서는 대충 어떤 정렬인지 짐작하기가 힘들다. 뭐 병합 정렬과 같은 경우는 뭔가 병합 해나가겠지 싶었는데 퀵 정렬은 아니다. 그래서 퀵 정렬이 무엇인가 라기 보다는 퀵 정렬의 작동 원리를 기록하는게 나의 인생에, 그대의 인생에 더 유익하지 않을까 싶다.

퀵 정렬은 병합 정렬과 매우 비슷하게, 쪼개는 것이 그 기본으로 깔려 있는 정렬이다. 또 쪼개기 시작한다는거다. 쪼갠다는 것의 의미는 병합 정렬에 잘? 설명되어 있는진 모르겠고 애타게 설명을 적어 놓았다.

https://typingdog.tistory.com/122?category=924874

퀵 정렬의 주된? 사상?은 이렇다. 

1. 배열을 쪼개는 것과 동시에 정렬하는 것이 아니다
2. 그렇다고 해서 앞/뒤 비교를 하며 정렬을 한다고 생각하면 안된다.
3. 어떤 기준에 맞는 '하나'의 요소의 정렬된 위치를 찾고, 고정한 뒤, 그 위치를 중심으로 양 옆 두개로 쪼개는 것이다. 이 때, 고정된 요소는 이미 올바른 정렬 위치를 찾았으니 정렬 대상에서 제외한다.

그러니까 결국에는 주어진 범위에 한해서 어떤 기준에 의거하여 단 하나의 요소의 올바른 정렬 위치를 찾아나가고 그 위치를 기준으로 양 옆으로 쪼개는 것을 반복해나간다고 생각하면 된다.

사과해야겠다. 이게 무슨 말이냐? 그림으로 기록해야겠다.

이런 배열이 있다.

이 배열을 아주 오도방정을 떨면서 왔다갔다 할 이상한 인덱스들을 소개하겠다.

자, 그림 내에 설명을 기록했지만, 추가 설명이 필요한 부분을 기록하겠다. 

일단, pivot은 비교의 기준이라고 했는데 꼭 이 기준을 맨 왼쪽에 둘 필요도 없다. 다만 이런 기준이 어디에 있긴 있어야한다는 소리인데, 오름차순 정렬의 경우 맨 왼쪽에 많이 쓴다고 생각한다고 생각한다....ㅋㅋ

left와 right는 무조건 배열 전체 중 인덱스 0과 인덱스 끝을 나타내는게 아니라 주어진 범위 내에서 가장 왼쪽과 오른쪽을 나타내는 것이기 때문에, 물결 표시로 강조를 했다.

기본적인 동작은 다음과 같다.

low와 high가 서로를 넘어선 경우이다. 이 경우에는 더 진행해도 (row의 입장에서)pivot보다 작은 값이, (high의 입장에서)pivot보다 큰 값이 나올리가 없기 때문이다. -> 우리는 지금 pivot을 기준으로 작은 값들을 왼쪽으로 몰아왔고, 큰 값들을 오른쪽으로 몰아왔다. 눈으로 잘봐라.

그러면 이제 몰려있는 곳의 경계가 있을 것이다. 3과 6 사이이다. 그 사이에 pivot 값을 넣고 뒤에 값들을 하나씩 땡기고 할 것 없이 high의 값과 pivot의 값을 바꾸면 정확하게 맞아떨어진다. 

pivot 기준으로 왼쪽은 pivot보다 작은 값. 오른쪽은 pivot보다 큰 값.

개쩐다.. 5가 고정 되었다. 이걸 재귀로 왼쪽편, 오른쪽 편 쫘르륵 실행해주면 알아서 각각의 pivot들이 제 자리를 찾아 정렬된 결과를 딱 보일 수 있을 것이다. 

이런 방법을 어떻게 생각했단 말인가 진짜..

코드 및 실행 결과

----

----

QuickSort 함수에서 ' if (left <= right) ' 이 조건! 이 조건은 위 퀵 정렬 과정에서 row와 high 가 서로 넘어서는 경우와는 완전 다른 조건이다. 해당 조건은 쪼개짐의 범위에 대한 조건으로 left와 right가 서로를 넘어서는 것은 이미 요소 하나 단위까지 쪼개고 난 이후라는 의미이다.

잘 정렬되었다. 

병합 정렬에서 재귀에 대해 한 번 설명을 써본 탓에 이번엔 정신이 온전하다.

퀵 정렬의 성능

퀵 정렬의 빅오는 pivot을 어떤 것을 선택하느냐에 따라서 다르다. 잘 선택한 경우

최선의 경우 : O(n log 2 n) - 2는 아래 첨자 2이다.
최악의 경우 : O(n^2) 

최선의 경우를 잘 뽑도록 pivot을 데이터 세트의 특성 상 잘 뽑아야하고, 데이터의 이동이 적기 때문에 매우 효율적이고 빠른 알고리즘이라고 생각하면 되겠다.

오늘도 역시 공부해놨던 부분을 이제 포스팅하는 시간이다. 역시 미리미리 해야한다.

스택이란?

일단 그림이 먼저다.

A, B, C 순서로 사각형을 넣을 것이다.

이렇게 된다. 그렇다면 다시 뺀다면?

이 때, 담는 용기, 통! 이것이 스택 자료구조이다. 
먼저 들어간 사각형 A가 제일 늦게 나오는 구조인 것이다. 이러한 개념을 후입선출이라고 한다. 나중에 들어간 것이 먼저 나오는 구조!

이를 구현하면 아래와 같다.

코드 및 실행 결과

---

---

중간 중간에 보완해야할 부분이 있지만 개념 부분에서는 충분하기 때문에 보완하지는 않았다.

이번에는 병합 정렬이다. 이게 생각보다 간단하긴 한데 복잡하다(?) 일단 시작한다.

병합 정렬이란?

병합 정렬의 기본은 다음과 같다.

1. 배열을 원소 단위로 쭉~~ 나눴다가
2. 다시 단계적으로 정렬과 동시에 결합을 반복한다.

그림으로 나타내자면 다음과 같다.

그럼 문제는 무엇이냐? 어떻게 쪼갤 것인가? 이다. arr[0] , arr[1] 이게 쪼갠 것 아닌가? 아니다. 그냥 원소에 접근한거지 쪼갠게 아니다. 

그럼 쪼갠다 라는 의미를 아주 곰곰히 생각해봐야한다. 

쪼갠다는 것은 큰 덩어리부터 시작해서 작은 단위로 나눈다는 것이고, 내가 원소 레벨까지 쪼갰다 라는 의미는 내가 지금 쪼개고 있는 진행 흐름이 원소 단위까지 접근했다! 라는 것이다.

좀 어렵지만 잘 생각해라. arr[0] 에 접근하는 것은 우리 집 강아지와 할머니도 할 수 있는 행위이다.(집에 강아지와 할머니는 없다) 이것은 쪼갠 것이 아니고 접근한 거다. 

쪼갠다는 것은 그림의 설명과 같다.

제어할 수 있는 인덱스 범위를 한정지으면 되겠다 이것이다. 그런데 내가 가만히 보니 이 쪼개는 단계가 범위만 줄어드는 것 외에는 모두 같은 짓을 하고 있는 것이다. 그렇다면 원본 배열을 던지고, 그와 함께 범위 값만 다르게 던져주면 알아서 쪼개주는 함수가 없으려나?

있다. 바로 재귀 함수이다. 바로 코드를 본다

위 함수처럼 원본과 범위를 지정하여 함수에 던져주면 알아서 반으로 쪼갤 것이다. 

위 그림처럼 될 것이다.

그렇다면 쪼갰으니 정렬과 결합을 해야한다. 다시 MergeSort 코드를 보겠다.

MergeSort는 범위를 나누어 두 토막 내고(2개의 MergeSort) 그리고 정렬과 결합을(Merge) 수행한다 라는 사실을 기억해야하며, 신뢰해야한다. 그니까 밑에 잔뜩 실행된 MergeSort 함수는 신경쓰지말고, 현재 주어진 범위들에 대해서 정렬하고 결합한다는 것이다.

위 그림처럼 밑 바닥까지 MergeSort 하면서 내려가면 더 이상 쪼개지 못하므로 각 MergeSort에게 지정된 범위에 대해서 Merge 를 통해 정렬과 결합을 수행해주고 리턴한다 그러면 한 단계 위층에서의 MergeSort들은 내부적으로 정렬된 두 덩어리를 받을 것이고 또한 그들도 Merge 를 통해 정렬과 결합을 수행해주고 리턴해준다. 언제까지? 다 합쳐질 때까지!

물론!!!! 여기서 정렬은 조상님이 와서 대신 해주는게 아니다! Merge라는 함수 내에서 이를 구현해야한다. 이는 어렵지 않으므로 코드로 확인해보면 될 것이다.

이 코드가 핵심인데, 앞 범위 토막과 뒷 범위 토막의 요소들을 모두 둘둘씩 비교하여 작은 값을 새로운 공간에 차곡차곡 넣는 방식이다. 이게 가능한 이유는 각 토막들은 아래 계층에서 이미 정렬되어 올라왔기 때문이다! (쓰면서 명확히 깨달음 ㅋ)

내가 무슨 말을 하고 있는지 모르겠다면 직접해봐라 미래의 나야

코드 및 실행 결과

----

----

머리가 참 아득해진다..

머리가 아득해지는 김에 빅오를 보자

병합 정렬 성능

최악/ 평균 / 최선에 상관없이 비교와 데이터 이동 연산을 모두 세어보면 O(n log 2 n)이다. 2는 아래 첨자 2이다.

오늘은 힙 정렬이다.

힙 정렬이란?

말 그대로 Heap 자료구조를 이용한 정렬 방식이다. Min Heap에서 루트 노드부터 빼오면 오름차순 정렬이 가능한 점을 이용해한 것이다.

힙 정렬은 Heap 자료 구조 조금 개조하면 만들 수 있다.
아래 그림과 같은 Min-Heap을 이용하면 정렬 성능이 죽여준다 ㅋ 

우선 순위 큐에서도 우선 순위가 높은 것을 작은 값이라고 약속하고 작성한다면 같은 결과이다. 뭐 그 기반이 heap 자료구조이니 heap을 통해서 구현했고, 이미 구현해놓은 것에 우선 순위 부분만 조금 수정하였다. 나중에 기억 안날 때에는 아래 링크 먼저 보고, 다음 코드를 확인하면 될 듯 하다. 

수정한 부분을 보자면, 원래 기존 heap 코드는 우선 순위를 결정하는 부분을 삽입마다 지정하기로 했는데 그것을 함수 포인터를 이용하여 없애버리고 자동으로 우선 순위를 나뉘도록 했다.

https://typingdog.tistory.com/110?category=924874

다음은 코드이다.

코드 및 실행 결과

----

----

힙 정렬 성능

힙 데이터 저장 시간 복잡도 : O(log2 n) - 2는 아래 첨자의 2이다.
힙 데이터 삭제 시간 복잡도 : O(log2 n) - 2는 아래 첨자의 2이다.
힙 데이터 정렬의 경우, 저장과 삭제를 각각 n번씩 수행하므로 시간 복잡도 : O(n log 2 n) - 2는 아래 첨자의 2이다.

힙 구조에 데이터 삽입, 삭제 등이 이루어진다는 것을 고려한다고 하더라도, 앞서 봤던 O(n^2) 정렬들 보다도 성능이 좋은 것이다.

하 코딩해놓고 묵혀뒀다가 포스팅하느라 다시 보고 시간 버리는게 너무 아깝다 앞으로는 정말 열심히 바로바로 정리해서 올려야겠다.

그래도 다시 복습할 기회가 되었으니 의미있는 시간이라 생각하고 일반 연결 리스트에 대한 기록이다.

내가 (윤성우 교수님의 자료구조 책의 ADT를 보고) 코딩한 연결 리스트는 살짝 형태가 다르다. 그러므로 특징에 대해서 그림과 글의 적절한 특징 설명 이후 코드와 실행결과를 기록 하겠다.

일단,

단순 연결 리스트란?

구조체와 주소 값을 이용하여 현재 노드 내부에 다음 순서 노드의 주소 값이 저장되어 있는 형태로 이 이어진 연결을 통해 값을 순회할 수 있는 자료 구조이다.

노드 내부에 다음 순서 노드의 주소 값이 저장되어 있다는 것은 이러한 경우를 뜻한다.

구조

원래는 아래 그림과 같은 형식으로 리스트가 구성되어졌어야 했는데 

머리 회전이 덜 된 관계로 아래 처럼 다른 리스트를 만들어버렸다. 그건 뭐 그거대로 기록할 것임.

일단 위 구조로 생겨먹었고, 노드 구조체와 그 노드들을 담고 관리하는 자료구조 구조체가 있다

새 노드가 항상 헤드 다음 즉, 실질 데이터 노드 맨 앞에 항시 존재해야만 한다. 값을 추가할 때, 값과 링크 값만 변경하고 사용한다. 위와 같은 특성 때문에 리스트를 초기화할 때 다음 그림과 같이 꼭 -1 값으로 초기화 한다.

초기화 및 추가

값을 추가할 때에는 빈 노드의 값을 변경하여 사용하지만, 그래도 어찌됐던 빈 노드를 헤드 다음, 데이터 노드들 맨 앞에 두는 것이 원칙이기 때문에 데이터를 추가할 때 빈 노드 또한 추가해 놓아야 한다.

순회
다음은 순회이다.

삭제 
다음은 삭제이다. 내가 따로 만든 함수들이 있기 때문에 간단하게 설명한다.

코드 및 실행 결과

----

----

메모리 관리가 중요한 것 같다.ㅋ