꿈 꾸는 누렁이

위 링크들에서 볼 수 있듯이 멀티 프로세싱의 주요 맥락을 확인하고, 포스팅하여 기록해보았다. 그런데 말입니다, 부모 프로세스와 자식 프로세스들 간에 통신이 필요한 경우는 어떻게 해야할까?

아니, 사실 프로세스들 간에 통신을 안 하는게 최고라고 나는 생각하지만 또, 그게 아닐 수 있으니 프로세스들 간의 통신 방법에 대해서 공부하고 넘어가는게 났겠다 싶어서 전에 공부를 해 보았다. 

일단, 프로세스들 간의 통신에 대해서 정리하기 전에 멀티 프로세스에 대한 정리를 한번 할 필요가 있다. 왜냐하면 이전 포스팅에서는 코드 구현 관점에서만 설명이 되어서 프로세스에 대한 충분한 설명이 이루어지지 않았다.

멀티 프로세스 개념 간단 정리

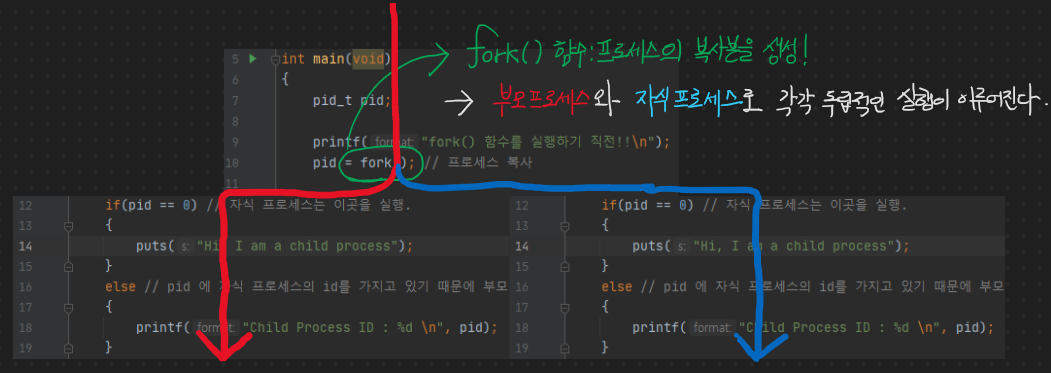
1. fork 함수를 통해서 프로세스가 복사되는데, 이 때, 복사라는 과정은 사실 새로운 프로세스의 생성 과정을 거친다.( PCB, Process Controll Block 이 함께 생성되어 생성된 프로세스에 대한 정보들을 저장하는 자료구조 블록이며, 컨텍스트 스위칭 때 이 정보를 활용한다)

2. fork 함수를 통해서 프로세스가 복사 시에는 부모 프로세스의 스택, 데이터, 힙 영역이 모두 복사되어 부모와 자식은 완전히 별개의 메모리 공간을 갖으며 내용 또한 그대로 복사된다.

자, 1번과 2번의 특징으로 인해서 프로세스 간에는 아무리 부모와 자식 사이의 관계라고 하더라도 서로 독립적인 메모리 공간을 가지고 있기 때문에 통신하기가 힘들다. 그래서 프로세스 간의 대화 방법으로 나온 것이 IPC이다. 

IPC란? 

IPC란 Inter Process Communication의 줄임말로 프로세스 간의 통신 방법을 의미한다. 

내가 공부한 프로세스 간 통신 방법은 다음 그림으로 설명할 것이다.

이게 바로 파이프를 이용한 프로세스 간의 통신을 간략하게 그림으로 그려본 것이다.

파이프의 생성은 위와 같은 함수로 진행된다. 운영체제에서 생성되는 공간이기 때문에 프로세스들과는 무관한 독립된 공간이고, fork 시 코드에 포함이 되어 있더라도 복제되는 메모리 공간이 아니다.

예제 코드 및 실행 결과

어떻게 데이터를 주고 받는지 부모가 자식에게, 자식이 부모에게 데이터를 주고 받는 경우를 예제로 확인해 볼 것이다.

29번 라인과 40번 라인의 sleep 함수에 대한 설명이 필요한 것 같다ㅋㅋㅋ 먼저, 29번 라인은 자식 프로세스에서 실행되는 영역에 sleep 함수를 넣었다. 왜 넣었을까?

먼저, 29번 라인에 sleep 함수가 없다고 생각하고, 28번 라인에서 입력 파일 디스크립터를 이용하여 값을 파이프에 집어 넣으 후, 31번 라인에서 바로 출력 파일 디스크립터를 이용하여 값을 파이프에서 빼내면 자식 프로세스 본인이 방금 넣은 값이 나올 확률이 높다. 36번 라인에서 부모 프로세스도 출력 파일 디스크립터를 이용하여 파이프에서 값을 빼내고 있으므로 자식 프로세스에서의 31번 라인과 부모 프로세스에서의 36번 라인 중 어떤 라인을 먼저 읽느냐에 따라 달린 것이기 때문이다. 아래와 같이.

그러나 29번 라인에서 sleep 함수를 실행함으로써 부모 프로세스가 먼저 값을 가져갈 수 있도록 여유를 두면 정상적으로 실행된다 다음처럼.

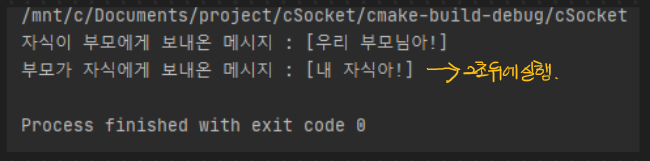
그리고 40번 라인의 부모 프로세스 실행 영역에서 5초 정도의 여유를 준 이유는 부모 프로세스가 종료하면 자식 프로세스도 함께 죽기 때문에 자식 프로세스가 충분히 부모가 전송한 데이터를 꺼낼 시간을 기다리기 위해서 5초의 여유를 준 것이다. 

그런데 이렇게 데이터를 넣고, 꺼내는 타임을 sleep 함수를 통해 실행 흐름까지 막아서 조정해가면서 행하는게 이게 프로그램으로서 말이나 된단 말인가?

아니, 그러면 애초에 부모용 pipe, 자식용 pipe 이렇게 구분해서

자식은 자식 파이프의 입력 디스크립터와, 부모 파이프의 출력 디스크립트만 사용하고,
부모는 부모 파이프의 입력 디스크립터와, 자식 파이프의 출력 디스크립트만 사용하면 된다.

다음 소스 코드와 실행 결과를 통해 볼 수 있다.

위와 같은 이런 모양새인 것이다.

이로써 IPC 까지 프로세스에 대한 내용은 모두 마친다.

이전 시리즈(?) 들이다.

이전 내용들을 토대로 멀티 프로세싱 서버를 구현해볼 것이다. 간단하게 특징있는 부분만 짚어본다.

시그널을 등록하는 코드.

파일 디스크립터와 소켓의 관계를 보여준다.

프로세스가 복제가 되면 서버 소켓에 해당하는 파일 디스크립터도 복제가 되고, 클라이언트 소켓에 해당하는 파일 디스크립터도 복제가 된다. 그렇지만 파일 디스크립터는 프로세스의 소유이고, 소켓을 가리키는 숫자에 불과하기 때문에 복제가 되도 상관없지만 소켓 같은 경우는 운영체제 소유이기 때문에 복제가 되지 않고, 복제 되어서도 안된다. 

그렇지만 소켓을 제거하려면 해당 소켓을 동일하게 가리키는 파일 디스크립터를 모두 제거해야한다. 부모든 자식이든. 그렇기 때문에 각 부모, 자식에서는 필요한 디스크립터만 살려두고 나머지를 제거해야 나중에 잊지 않고 완벽하게 소켓을 제거할 수 있다.

전체 코드 및 실행 결과

지난 번 포스팅에 이어서 작성한다.

fork 함수를 통해서 프로세스의 복사본을 생성할 때는 꼭 중요한 규칙이 있다.

자식 프로세스가 종료되면 이 자식 프로세스의 반환 값을 부모 프로세스를 반환 받아야만
자식 프로세스가 메모리 상에서 아예 소멸될 수 있다.

그러니까 자식이 행한 모든 행위는 부모가 책임져야 한다 와 비슷한 이야기인 것이다...ㅋㅋㅋㅋ 이 때, 반환이라함은 return이나 exit(n) 함수를 자식 프로세스에서 실행하여 반환하는 것을 의미한다.

좀비 프로세스의 등장

그렇다면 이러한 규칙을 어기게 된다면 어떻게 될까? 그것은 다음의 코드를 보면 된다.

좀비 프로세스란? 메모리 상에는 있지만 아무 기능을 못하는 상태로 자원만 할당하고 있는 채로 있는 상태를 이야기 한다. 즉, 말 그대로 좀비인 프로그램인 것이다.

지금 부모가 낳은 자식인 자식 프로세스가 종료를 했지만 종료하지 못하고, 좀비 형태로 남아있다는데!! 이게 무슨 말인가? 왜 이런 현상이 발생했는지 다음의 그림을 보면 된다.

결국, OS 개입과 5번 처럼 부모의 OS에게로 요청이 없기 때문에 자식은 좀비 형태로 살다가 죽게되는 것이다ㅠㅠ. 

좀비 프로세스의 해결방안

그래서 이러한 좀비 프로세스 문제를 해결하기 위해서 약 3가지 정도의 해결 방안들이 제시된다. 이러한 방법들의 근본은 자식 프로세스의 반환 값을 부모 프로세스에게 전달되도록 해주는 과정들이라는 것이 공통 근본이다.

1. wait() : wait 함수를 실행 함과 동시에 현재 메모리 상에 존재하는 종료 '처리' 된 자식 프로세스를 탐지하여 순서대로 반환 값을 얻어내고 종료 '처리'된 자식 프로세스를 소멸시킨다.

단, wait() 함수는 블로킹이다 ㄷㄷ. 즉, 종료 처리된 자식 프로세스가 없다면 부모 프로세스의 실행 흐름이 멈추고 대기한다는 소리이다. 매우 치명적이다 .. ㅋㅋ 

주석을 조금 상세히 적어놨다. 읽으면 될 것이다.

2. waitpid() : waitpid 함수는 wait과 본질적인 역할은 동일하나, 블로킹이 없다!!!

역시 마찬가지로 주석을 읽으면 이해에는 문제가 없다.

3. signal(), sigaction()

이전의 방법들은 부모 프로세스에서 자식 프로세스가 종료 처리가 될 때를 대비해서 꼭 wait 함수나, waitpid 함수를 통해서 종료 처리된 자식 프로세스가 존재하는지 탐색하는 과정을 거쳤다.

그런데, 자식 프로세스가 언제 종료될지를 모르기 때문에, wait이나 waitpid 류의 함수를 주기적으로 계속 실행시켜서 확인을 해야한다. 이는 매우 비효율적이다.

그래서 사람들은 해결책으로 이러한 생각을 한다.

1) 아니 그러면 운영체제가 자식 프로세스가 종료 처리되는 걸 뻔히 알고 있으면서
말도 안 해주는게, 이게 사람 새끼냐?( 팩트> os는 사람 아님 )

2) 그러지말고, 자식 프로세스가 종료 처리되는걸 운영체제는 알고 있으니,
운영체제는 자식 프로세스가 종료 처리되는 순간이 오면, 그걸 부모 프로세스에게 알려주자!

3) 이 때 부모 프로세스는 자식 프로세스의 반환 값을 회수 처리하는 로직을 담은 함수를 만들어서
운영체제에게 등록해놓아라.

4) 그러면 운영체제가 그 알려주는 방법으로 부모 프로세스가 등록해놓은 함수를 실행하는 것으로 하면 되지 않겠냐?

기가 막히고 참된 효율적인 대화이다..

그래서 등장한 것이 signal(), sigaction() 이 함수들인데, 같은 역할을 하지만 signal 함수는 유닉스 별로 다르기 때문에 사용되지 않으며 호환을 위해서만 남겨져 있다. 그래서 sigaction() 이라는 함수를 통해 시그널을 등록하는 과정을 아래에 예제로 보일 것이다.

자식 프로세스가 종료되고 바로 소멸까지 이어지는 모습을 확인할 수 있다.

비로소 좀비 프로세스 상태를 막을 수 있는 방법들을 살펴봤다.

진짜 다 까먹어서 다시 예제 쳐보고 다시 올린다... 정말 미리미리 올리고 자주자주 봐야합니다..

포스팅 순서가 사실 멀티 프로세싱이 먼저이지만, 게임 서버 개발에 사용한 것은 멀티 플렉싱 모델이었기 때문에 먼저 올렸었는데, 사실 멀티 프로세싱이 무엇인지, 그리고 그 단점이나 필요한 영역은 어느 부분인지 알아야 한다.

그래서 포스팅을 또 하게 되었다.

내가 구현했던 서버의 모델은 멀티 플렉싱 모델이었다(select, epoll) 이 모델은 위와 같은 구조로 이루어진다.

여러 학생들이 클라이언트들이고, 교사는 하나의 프로세스이다.
질의와 답변을 필요로 하는 학생들, 즉 송수신을 요청하는 애들만 빠른 반복문 처리를 통해 처리한다.

이러한 모델에서는 여러 명의 클라이언트들이 송수신이나 연결 등의 여러 요청을 할 때마다 그 요청만큼만 처리하는 구조이기 때문에 대용량의 파일을 송수신하는 연결과는 적합하지 않다. 

반면, 멀티 프로세싱 모델은 다음과 같다.

교사들은 프로세스들이고, 여러 학생들이 클라이언트들인것이다.
학생들이 질의와 답변을 필요로 하든 안 하든 무조건 프로세스와 연결되어 1대1 통신이 진행되는 것이다.

이런 구조에서는 시간이 오래 걸리는 상담이나 컨설팅 같은 서비스가 교사와 학생들 사이에서 제공되어야 할 법하다. 마찬가지로 프로세스-클라이언트 입장에서 봤을 때, 용량이 크고 시간이 오래 걸리는 파일 전송 등이 자원 효율이 클 것이다.

이러한 멀티 프로세싱 기반의 소켓을 작성하기 위해서는 fork() 에 대한 개념이 필요하다.

그전에! 프로세스란 무엇인가?

운영체제 관점에서 별도의 실행 흐름을 구성하는 단위. 
생성될 때, PCB(Process Controll Block) 라고 하는 프로세스에 대한 정보 구조가 생성되며,
이 정보에는 해당 프로세스에 대한 구체적인 정보들이 저장된다
(메모리 할당, 파일 디스크립터 테이블 등등 수 많은..)

프로세스의 복사본을 생성하는 fork()

위와 같은 기본 코드가 있다. 10번 줄을 보면 fork 라는 함수를 호출한다. 이 fork() 함수는 프로세스를 그대로 복사하는 함수이다. 이 함수가 호출되는 순간!! 프로세스가 그대~로 복사되어 10번 라인부터는 흐름이 각각 따로 진행된다. 다음과 같이 말이다.

그렇다면 이 함수가 반환하는 값은 무엇일까? 원래 실행되던 흐름을 부모 프로세스라고 하고, 복사된 실행 흐름을 자식 프로세스라고 한다.

부모 프로세스의 실행 흐름일 때, 10번 라인에서 반환되는 값은 자식 프로세스의 프로세스 ID 번호이다.
자식 프로세스의 실행 흐름일 때, 10번 라인에서 반환되는 값은 무조건 0이다.

그래서 12번 라인과 16번 라인에서는 부모 프로세스와 자식 프로세스의 실행 흐름을 구별하기 위해 pid를 0인지 아닌지를 비교하고 각 실행 흐름에 맞는 처리를 진행하면 된다.

이런 식으로 프로세스를 생성하므로, 클라이언트가 접속하면 프로세스를 복사하여 클라이언트에게 할당해줘서 송수신처리를 담당하면 된다. 

그런데.. 이러한 방식에는 큰 문제가 있었으니..

이번 포스팅에서 제일 중요한 것은 프로세스의 복사는 아예 메모리까지 통채로 복사되어
실행 흐름이 완전 다른 별개로 나뉘어진 부모 프로세스, 자식 프로세스라는 것이다!

미루고 미뤄왔던 보간 탐색에 대한 포스팅이다!!!

위에는 보간 탐색의 기반이 될 탐색의 원리를 설명해 놓은 글이다. 무려, 4개월 ~ 5개월 전에 내가 작성했던 글이다. 지금 봐도 상당히 디테일하게 잘 작성한 것 같은데 , 코드라던가 실행 결과 등을 제대로 올리지는 않았더라.

그래서 이번 포스팅에서 보간 탐색과 함께 이진 탐색의 재귀적 구현, 이진 탐색의 반복문 구현까지 원쁘라스투(1+2) 형태로 포스팅 들어간다.

먼저, 보간 탐색이 Main 이니 보간 탐색에 대해 살펴보도록 한다.

보간 탐색이란?

이진 탐색을 살짝 더 효율적으로 개선한 것이다! 기존의 이진 탐색의 경우 다음과 같이 탐색이 진행되는데,

3번의 이진 탐색이 진행되었고, 그 3번의 이진 탐색 안에는 수 많은 계산들과... 수 많은 조건 검사 등으로 인해 그냥 선형 순차 탐색만도 못한 효율이 나와버렸다. 그 이진 탐색 시켜주려고 정렬까지 한 것을 생각해보면 억울하다. 

물론.. 미미한 성능 차이이고, 데이터가 더 많고, 타겟이 더 안쪽에 있었을 때에는 분명히 이진탐색이 개쩔긴하다ㅋㅋ 예를 들기 위해서 극단적으로 말해본 것이다.

왜 위와 같이 선형 순차 탐색보다도 못한 결과가 일어났을까? 왜냐하면...

첫 번째, 데이터가 생각보다 앞에 있었기 때문이다.
두 번째, 죽으나 사나 수행하는 반 절 나누기로 인해서 절반 지점부터 시작하는 탐색 시작 위치가 문제이다.

그래서 데이터가 극 초반이나, 극 후반에 존재할 경우에도 계속 반절부터 시작할꺼냐! 라는 생각에서부터 시작되었다.

첫 번째 원인은 타겟이 치우져 있는 것은 우리가 어떻게 할 수 없는 것이다. 사용자가 찾겠다고 하는 타겟이 거기 있는걸 무슨 수로 해결하는가?

그렇다면 두 번째, 앞으로 절반 지점부터 시작하지 않으면 되지않을까? 

그래서 이렇게 바꿔봤다. 이 공식은 아마도 수학 센세들이 힘들게 연구한 공식이 아닐까 한다. 저 공식은 

"내가 찾는 값과 그 값이 저장되어 있는 위치는 비례하기 때문에 전체 길이에서
대충 이 정도 어디쯤에느으으은~~ 있지 않겠는가?"

를 이야기하는 공식이다. 그럴 수 밖에 없는게 이진 탐색과 마찬가지로 정렬되어 있는 데이터 세트를 대상으로 하기 때문에 당연히 전체 길이에서 찾으려는 값은 어림잡아 이쯤에 있겠거니 하고 추측해볼 수 있는 것이지 않겠는가?

그래서 그걸 실제로 구현해 본 예이다.

그런데 다음과 같은 예에서 탈출 조건에 문제가 있다. 

위의 조건대로 데이터 세트와 타겟을 2로 조정하여 실행해보면 실행이 무한 루프에 빠진다. 즉, 탈출 해야하는데 탈출 조건을 충족시키지 못해서 무한 루프에 빠지는 것이다.

그렇다면 왜 이전 탈출 조건인 start <= end 조건은 먹히지 않는걸까? 그 이유를 아래에 정리해 보았다.

그도 그럴 것이, 새로 정의된 공식으로 인해서 정해지는 index 값은 "너가 찾는 타겟 값은 전체 길이 중에 대충 어디어디 쯤에 있어~" 라고 이야기해주는 것과 같다. 그렇다보니, 아무리 start 와 end 가 갱신된다고 하더라도 이전과 비슷한 index 값을 계산해서 내놓을 확률이 높다. 더군다나 start가 1밖에 증가하지 않은(범위가 겨우 인덱스 하나 줄어든) 상황에서는 더더욱 그럴 확률이 높다. 이런 와중에 갱신된 범위가 target이 포함되지 않는 상황까지 되어버린 것이다. 그러면 아주 그냥 삼위일체이다.

위의 예시 상황으로 보자면 다음과 같은 입장들이 되는 것이다.

새 공식 曰 : target 2는 인덱스 0 쯤에 있어~, index = 0 ~
start, end 曰 : 오 마침 index가 0이고 index+1이 start로 넘어오니 결국, 범위가 하나 밖에 안 줄었네?
arr[start], arr[end] 曰 : 3 ~ 9 값이군.
target 曰 : 난 2인데!!!! 왜 3 ~ 9를 보고 있냐!!! 다음 재귀 호출 때 탈출해라!!!
                   [ 재귀 호출 ]
탈출 조건 曰 : 응~ start <= end 조건 성립해서 탈출 안 해 ~
새 공식 曰 : (범위가 하나 줄은 것 가지고는 결과는 그대로겠네..?) 음.. 뭐.. target 2는 인덱스 0쯤에 있어~, index = 0 ~
                   [... 무한 반복 ...]
컴파일러 曰 : '신발장 크레파스 놈들이!!!!!!!!!!!!!!!!!!!!! 꽥(무한 루프 터.짐.)'

위의 대화가 탈출 조건과 새 공식의 순서가 코드와 조금 다르긴 하지만 문제는 없다. 결국은 같기 때문이다.

뭐 위 대화까지 보고도 이해가 안된다면 내 잘못이다. 설명을 못한 것이다. 근데 이게 글로만 설명하기 겁나 애매하고 짜증난다 ㅋㅋㅋㅋㅋㅋㅋㅋㅋ

아래는 코드와 실행결과이다. 탈출 조건까지 최종 수정된 보간 탐색과 이진 탐색의 재귀적 구현과 반복적 구현까지 모두 넣어 놓은 3종 세트인 것이다.

코드와 실행 결과

없는 값으로 인해 탐색 실패 결과

탐색 성공

기수 정렬이다. 드디어 정리할 시간이 다가왔다.

Q. 기수 정렬에서 기수란 무엇인가?

A. 숫자 표현(진법체계)에 기준이 되는 수를 뜻한다. 예를 들자면 16진, 10진, 8진, 2진 등을 기수라고 한다.

Q. 그럼 기수 정렬은 무엇인가? 기수를 통해서 어떻게 정렬을 이뤄내는가?

A. 예제를 통해서 보겠다.

정렬이 되는 대상들을 하나의 진법 속 요소들로 가정하고,

해당 진법 배열에 값을 모두 넣은 후, 단순히 순서대로 꺼내기만 한다.

이런 식으로 동일한 기수의 요소들끼리 해당 기수의 버킷을 이용하여 정렬이 이루어지는 것이 기수 정렬이다.

중요한 것은 해당 기수의 버킷에 넣고 다시 버킷의 처음부터 순서대로 꺼낼 뿐이다. 그러니까 값의 비교가 이루어지지 않는다는 것이다! 그렇기 때문에 정렬할 대상들에 따라 반복문을 여러 번 사용해야할 수도 있고, 중간에 갑자기 진행을 끊을 수도 있으며, 정렬할 수 있는 대상이 제한이 되기도 한다.

예를 들어, 1, -5, 100 이런 요소들에 대해서는 정렬이 불가능하다. - 를 기수 버킷으로 어떻게 표현할 것이란 말인가?

다음으로 간단한 숫자 정렬하는 예제를 보겠다.

코드 및 실행 결과

지난 이야기..

문제점

뭐 위와 같은 문제들이 있다. 위의 문제의 전제는 등록되는 수는 100명도 안되고, 거의 그대로지만 번호만 오지게 큰 스케일로 변환되는 경우이다. 

해결 아이디어

그러면 어떻게 하면 될까? 

큰 인덱스 키 값의 크기를 줄이면 된다!

<인덱스를 축소 변환하는 과정>

1. 어차피 등록되는 인원은 100명이 안될 것이기 때문에 20171300 ~ 20171399 라고 범위를 어림 잡는다 
2. 그러면 말이 20171300 부터 20171399까지 이지 결국엔 0부터 99까지라고 봐도 문제가 없다.
3. 그렇다면 인덱스를 대입하기 전에 20171300이 오면 무조건 0으로 변환해주고, 20171344가 오면 무조건 44로 변환해주며, 20171399가 오면 무조건 99로 변환해주어 인덱스에 대입되도록 하면 어떨까?
4. 등록번호 % 100 을 한 결과라면 무조건적으로 위의 결과를 얻는다.
5. 그렇다면 user acc[100] 을 그대로 넣고 acc[uid%100] 으로 접근하면 배열의 크기를 비정상적으로 늘리는 고민을 해볼 필요도 없게되는 것이다.

이러한 과정에서 축소 변환해주는 역할을 하는 것을 해쉬(hash)라고 하며, 해당 역할을 하는 함수를 해쉬 함수라고 한다.

해쉬 함수는 다음과 같다. 겁나 간단하다.

이러한 해쉬 함수는 위에서 밑줄 친 것처럼 다양한 값의 형태에 따라 달라진다. 해쉬되어야 할 키 값의 상황? 문맥? 에 따라서 적용되는 해쉬 함수의 내용이 달라지고, 정답이 없다는 뜻이다.

적용된 코드 분석

등록을 할 때에 hash 함수를 이용하며,

값을 꺼낼 때에도 hash 함수를 이용하여 인덱스를 축소 변환하여 인덱싱한다.

전체 코드 및 실행 결과

그런데 또 문제점

짜증나게 또 문제가 발생하는 것이다.. 이번엔 등록해야하는 수가 갑자기 늘어나 버려서 다음과 같은 현상이 발생하는 것이다. 

1. 한 200명~300명 정도 난다.
2. 그래서 배열의 길이를 넉넉하게 user acc[400]; 정도로 주었다.
-> 이 방법 또한 썩 마음에 들지 않는다. 왜냐하면 등록 수가 늘어날때마다 계속 변경을 해줘야 하기 때문이다.
3. 그런데 문제는 여기서부터이다. 20171350과 20171450의 해쉬 결과는 50으로 같다.
-> 왜냐하면 100으로 나눈 나머지이기 때문에!(직접 나눠보라)
4. 20171350 등록 번호인 사람과 20171450 등록번호인 사람의 해쉬 결과가 50으로 같으므로 둘다 acc[50]에 정보가 등록될 것이다.. 그러니까 먼저 저장되는 값은 손실 된다는 의미이다. 원래 기대 결과는 20171350은 [50]에 20171450은 [150] 에 저장되는 것을 기대했는데 말이다.

지금 두 가지 문제가 발생하였다.

첫 번째는 문제는 등록되는 수가 넘쳐날 때마다 테이블의 크기를 갱신해야하는 상황이 발생한다.

두 번째는 문제는 분명히 다른 등록번호임에도 불구하고, 해쉬된 결과로 같은 인덱싱 번호가 나왔다. 

먼저, 두 번째 문제와 같이 같은 해쉬 결과가 나오는 것을 충돌(Collision)이라고 한다. 이러한 충돌을 막으려면 어떻게 해야할까? 해쉬 함수를 기가 막히게 잘 만들어야 한다. 해쉬 함수는 해쉬하려고 넘어오는 키 값의 범위나 종류나 형태, 양상에 따라 달라질 수 있기 때문에 매우 주관적이며, 답이 없다. 

A회사에서 만든 해쉬 함수가 기가 막히게 성능이 잘 나오다가도 B회사에서 A회사의 해쉬 함수를 쓰면 동작이 잘 안될 수도 있다. 그렇지만 최대한 공통으로 적용할 수 있는 여러 알고리즘? 들이 존재한다.

자릿수 선택, 폴딩 방법, 선형 조사법, 이차 조사법, 이중 해쉬, 체이닝 ... 등

이렇게 여러 방법들이 존재하지만 이 방법들의 공통점은 해쉬 해야할 키 값을 어떻게 변환해야 충돌이 덜 일어나는가에서부터 시작하는 방법들이다.

가장 좋은 해쉬 방법을 만드는 것은 키 값의 부분을 활용하여 해쉬된 키 값을 만들 것이 아니라, 키 값의 전체를 활용하여 해쉬된 키 값을 만들어야 한다는 것이다.

위의 예제에서도 키 값의 마지막 두 자리 수만 가지고 장난질 했기 때문에 문제가 되었다. 키 전체를 활용할수록 콜리전이 발생할 확률이 매우 낮아진다.

첫 번째 문제는 해쉬 함수의 구현에 따라 달라진다. 해쉬 함수를 통해 변환되는 해쉬된 키 값의 범위를 어떻게 정하느냐에 따라 적절한 할당 크기를 정할 수 있기 때문이다.

테이블과 해쉬 등은 성능은 좋지만 이러한 충돌(collision) 문제로 인해, 그리고 키를 이용하여 제어해야하는 곳에서만 주로 사용해야하기 때문에 사용되는 곳이 제한된다. 

테이블과 해쉬를 살펴봤는데 해쉬 테이블은 기본 동작 원리나 문제점 그리고 적용 가능한 작업의 특징 정도로만 공부하고 넘어가는게 좋을 것 같다.

자 오늘은 테이블과 해시이다.

자료구조는 자료를 저장하는 구조를 나타내는 것이지만, 그 구조 속에 들어 있는 값을 찾아서 꺼내는 것 또한 자료 구조의 영역 범위 내이다.

그래서 배열 리스트, 연결 리스트, 스택, 큐, 그래프, 트리 등에서 탐색에 해당하는 부분을 구현해왔다. 그 중 테이블이라는 자료구조에 대해 볼 것인데, 이 구조는 특별하다. 탐색 속도가 어마어마하게 빠르다. 기록해보자.

테이블이란 무엇인가?

이것이 테이블 자료구조이다. 키와 값으로 구성되어 있는 구조를 테이블 자료구조이다. 보통 언어에 따라 다르지만 키와 값으로 구성되어있는 자료구조를 사전(Dictionary), 맵(Map) 구조라고도 한다.

테이블 자료 구조에서의 핵 중요한 규칙

1. 테이블 자료구조에서는 키와 값이 한 쌍의 형태로 이루어 저장이 된다.
이 때 값은 뭐 하나가 되어도 좋고 여럿이 되어도 좋다.

2. 테이블 자료구조에서는 키 값은 중복되어서는 아니 된다.
아래의 그림을 보자

학생을 관리하는 테이블이다. 소위 말하는 학번이라는 것은 각 학생들에게 부여되는 고유 번호이다. 그러니까 학번 1번을 외치는 것만으로도 수 많은 학생들 중에서 '나루토'를 특정 지을 수 있어야한다. 이것이 실생활에서 적용되는 예이다. 

그런데 위의 테이블에서 학번 3번을 부르면 네! 하고 손을 드는 학생이 에렌과 아르민으로 두 명인 상황이 만들어졌다. 이런 경우에는 학번을 부르고 나서 이름까지 불러야 그제서야 에렌과 아르민을 특정 지을 수 있는 것이다.

만약 이런 상황에서 3번으로 중복되는 에렌과 아르민이 포함되어 있는 전교생 수천명이 시험을 본다고 생각하자. 그러면 자동적으로 OMR 채점을 진행할텐데 이 때 기계는 각 학생들을 구분할 때, 학번을 이용하여 학생을 특정 짓지만 에렌과 아르민 자식들이 포함되어 있는 경우가 존재하기 때문에 모든 학생들을 대상으로 학번과 이름을 한 번에 확인해야한다.

테이블 자료구조에는 보통 키 값을 이용하여 데이터를 특정짓기 때문에 위와 같은 경우를 만들지 않기 위해서 키의 중복을 허용하지 않도록 하겠다. (뭐 허용을 시키는 경우도 있긴 하지만 말이다.)

3. 키가 없으면 값을 저장할 수 없다.

키를 활용해 값을 특정 지어야 하기 때문에 키를 비울 수는 없다.

4. 값을 특정 짓는다는 것의 의미.

위 그림을 봤을 때, 3번이라는 학번을 통해 에렌을 특정 지었는데 달리 말하면 탐색이 완료되었다는 소리이다. 

이 개념들을 숙지한 채로 아래의 예시를 보면 된다.

기본적인 테이블 예시

테이블이 될 구조체 정의

구조체 정의를 이용하여 배열로 선언하면 테이블 형태의 구조를 만들 수 있다.

테이블에 데이터를 등록하는 함수

인덱싱이 특이하다는 것을 확인할 수 있다.

메인 함수 실행 부분

임의로 입력된 값을 키 값으로 활용한다.

49번 줄에서는 키 값을 이용해 원하는 값을 바로 뽑아낸다. 이런 것이 가능한 이유가 무엇인가? 

데이터를 삽입할 때, 키의 값 '번째'에 해당하는 배열 칸에 넣었으니,

값을 뽑아올 때에도 키를 인덱스로 던져주면 키의 값 '번째'에 해당하는 배열 칸에서 뽑아온다.

말이 탐색이지, 사실 탐색이라고 할 것도 없이 그냥 인덱싱일 뿐이다. 그냥 *(배열이름+인덱스(키값)) 이렇게 연산해주면 접근 가능하기 때문에 포스팅 초반에 겁나 빠르다고 한 것이다.

전체 코드 및 실행 결과

문제점

근데 위와 같은 테이블은 빠른건 빠른거지만 중요한 문제가 있다.

1. 학번이 원래 0부터 100까지의 자리였지만 갑자기 년도+번호와 같은 식으로 변해버리면 분명히 문제가 된다.
원래 99번이었던 번호가 20210099로 바뀐다면 이 또한 문제가 될 것이다. 

기존의 방법대로라면 user acc[20210100]; 이렇게 선언을 해야, 20210099 같은 인덱스가 먹혀도 먹힐 것이다. 그런데 이러한 크기의 배열 선언이 과연 정상일까?

모든 키가 0부터 시작해서 뭐 적절히 1,000 값으로 끝나면 좋겠지만 실제로는 그렇지가 않다. 학번은 보통 해당 년도와 고유 번호를 합쳐서 만든다. 군번은 말할 것도 없다 이런 번호 키들을 수용하기 위해서 user acc[20210100]; 이렇게 비정상적인 배열 선언을 할 수도 없는 노릇이다.

이를 다음 포스팅 때 해결하고자 한다.

앞선 내용들을 바탕으로 진행하기 때문에 읽고 나서 읽는 것을 추천한다. 설명을 잘 하지 못해서 읽어도 모를 수도 있다. 이 글들은 복습을 위한 기록이니, 잘 못 알아 듣겠으면 다른 곳 가서 읽기를 권한다ㅋㅋㅋㅋ ㅜㅜ

일단 먼저 BFS가 뭔지에 대한 내용은 위 링크 중 땡땡 우선 탐색이라는 글에 좀 더 자세하게 정리되어 있고, 이 글에서는 BFS 방법으로 순회하는 과정을 나타낼 것이다.

중요 핵심

일단 너비 우선 탐색은 깊이 우선 탐색과 달라도 너무 다르다. 현재 정점 하나에 연결되어 있는 모든 정점에 순회를 해야하다보니 현재 정점에 연결된 각 정점마다 순서를 매겨서 기록해야 한다.

깊이 우선 탐색은 현재 정점에서 다음으로 갈 타겟을 정하기만 한다면 정점 방문(순회)과 현재 정점의 갱신이 한 번에 발생한다. 

그러나 너비 우선 탐색의 경우에는 정점 방문이라는 개념을 좀 더 확장해야한다. 단순히 방문만 하는 것이 아니라, 방문 후에 방문한 해당 정점을 큐 자료 구조에 넣는 작업까지가 정점 방문이라고 생각해야한다.

그리고 정점 방문과 현재 정점의 갱신이 동시에 발생하지 않는다. 정점 방문과 현재 정점의 갱신을 동시에 해버리면 나머지 연결되었던 정점에 접근할 기회가 박탈된다.

위의 예에서 현재 정점이 0이고 (ㄱ, ㄴ)처럼 1 정점을 방문한 뒤 바로 현재 정점으로 갱신을 해버리면 0 정점에 연결되어 있던 2 정점에 접근할 수 있는 기회가 사라진다. 그렇기 때문에 정점의 방문과 현재 정점의 갱신이 동시에 발생하지 않는 것이다. 

이러한 이유 때문에 진짜 설명하기에 겁~~나 헤깔린다. 이러한 핵심적인 특징을 인지한 상태로 프로세스를 봐야한다.

순회 프로세스

먼저 다음과 같은 그래프에서 순회를 시작할 것이다.

정점 0은 시작 정점이므로 일단 방문 처리가 자동으로 된다. 정점 방문에 해당하는 부분이 순회라는 표현이고, 이는 접근 + 큐 기록 까지를 의미한다. 접근했다는 의미 또한 방문 Flag 배열에 값을 갱신하는 조작을 의미하는 것이다.

현재 정점에 연결된 모든 정점을 순회하는 과정이다.

현재 정점인 0 정점에 연결된 모든 정점에 대해서 순회가 완료되었으니, 큐에서 값을 꺼내서 그 값을 현재 정점으로 갱신하고, 다시 순회를 시작한다.

그리고 큐에 정점이 여전히 존재하므로 다시 큐에서 값을 빼내어 현재 정점을 갱신하고, 순회를 재시작한다. 그런데 2 정점 같은 경우는 순회 가능한 인접 정점이 없으므로 그냥 나가리~

큐에 정점이 여전히 존재하므로 다시 큐에서 값을 빼내어 현재 정점을 갱신하고, 순회를 재시작한다. 4 정점이 마지막 정점이긴 하지만 그림을 한 눈에 보는 우리나 아는 것이지 컴퓨터는 4 정점이 마지막 이라는 것을 아직 모른다! 그렇게 때문에 4 정점이 마지막이어도 원래 규칙대로 큐에 넣는다.

큐에 정점이 아직 존재하니 뽑고, 뽑힌 값으로 현재 정점을 갱신한다. 그런데 현재 정점에서 순회를 하려고 보니, 순회 가능한 인접 노드가 없다. 

그렇게 더 이상 큐에 값을 넣지 못하고, 큐가 비었으므로 모든 그래프를 순회했으므로 종료한다. 

0 -> 1 -> 2 -> 3 -> 4 순으로 순회가 이루어졌다.

진짜 뇌리에 박히겠다 박히겠어 정말 ㅋㅋ

이제 관련된 부분 코드를 보도록 하겠다.

코드 분석

큐가 새롭게 사용되므로 큐에 대한 코드가 필요한데 이미 만들어놓았던 배열 기반의 큐 코드를 활용할 것이다. 그런데! 그냥 큐는 배열 관리가 까다롭기 때문에 더 효율적인 배열 기반의 원형 큐를 사용할 것이다!

깊이 우선 탐색 코드에 대해서 바뀌는 부분과 추가되는 부분을 기록하겠다.

너무나도 기쁘게도 이거 하나가 변경된다.

ㄱ~ㅅ 순서대로 읽으면 된다.

전체 코드 및 실행 결과

전체 코드는 배열 기반의 원형 큐와 연결 리스트 BFS로 인해 변경된 그래프 코드 순으로 업로드를 하겠다.

배열 기반의 원형 큐 ArrayBasedCircleQueue.h -- -- -- -- -- 

연결 리스트 linkedlistforgraph.h -- -- -- -- --

BFS 로 인해 변경된 그래프 코드 BreadthFirstSearchGraph.cpp -- -- -- -- --

아래는 실행 결과이다.

이 두 탐색을 이용한 최소 비용 신장 트리 부터 해서 트리 부분의 AVL 트리, 해쉬 테이블 등등 더욱 복잡한 것들은 지금까지 포스팅 한 것들을 복습한 이후에 조금씩 업로드를 진행할 것이다.

그노므 DFS! DFS! 드디어 깔끔하게 정리를 한다. 이 탐색 기법 하나에 워낙 들어가는 내용이 많기 때문에 바로바로 정리하지 않으면 다시 처음부터 공부하는 수준으로 공부를 해야한다 흑흑...

이전의 포스팅의 내용을 기반으로 작성되기 때문에 이전 부분을 포스팅을 참고하라고 올려놓겠다.

중요 핵심

일단은 깊이 우선 탐색은 아래 세 가지가 핵심이다.

1. 깊이 접근하는 것
2. 왔던 경로를 되돌아오는 것
3. 정점 방문 여부를 기록하는 것

이 세 가지를 핵심으로 기록하겠다. 사용되는 예시는 간단하게 다음과 같다.

첫 번째, 깊이 접근한다는 것은 한 정점에서 연결되어 있는 정점 중 하나의 정점을 선택해서 파고 들어가고 또 그 정점에서 연결된 정점 중 하나의 정점을 파고 들어가는 식의 방법을 이야기 한다.

1로 갈지, 2로 갈지는 중요하지 않다. 0이라는 정점에 연결 되어 있는 정점이 1 먼저 연결되있는지, 2 먼저 연결 되어있는지에 따라 다르다. 즉, 정점의 연결 정보를 나타내는 연결 리스트의 정렬 구조에 따라서 1 노드와 2 노드 중 어떤 것을 선택하게 될지 결정된다는 소리이다. 어찌됐건 우리는 순회 하는 것이 목적이므로 어딜 먼저 방문하는지는 의미가 없다.

두 번째, 왔던 경로를 되돌아오는 것은 되돌아오면서 놓친 정점을 순회해야하는 것이다. 이 때 경로를 다시 되돌아오려면 경로를 일단 기록을 해야하는데 역행이므로 스택의 형식대로 기록하면 된다. -> 방문 추적을 목적으로 스택을 사용한다.

세 번째, 정점 방문 여부를 기록한다는 것은 일반 순차 배열을 이용하여 기록한다. 다음 그림에 설명을 포함시키겠다.

주요 3가지 핵심에 대해서 살펴보았고 이번엔 그 순서대로 그려볼 것이다...

순회 프로세스

시작 정점 0을 방문된 상태로 시작한다. -> 방문 Flag 배열에서 정점 0을 True 처리.

연결된 인접 정점은 1 정점과 2 정점인데 방문 Flag 배열을 봐도 방문 처리가 False이기 때문에 두 정점 모두 접근이 가능하다. 이 예에서는 2 정점을 방문하겠지만 1 정점으로 방문해도 순회 순서만 다를 뿐 다른 의미는 없다.

2 정점을 방문하면서 방문 Flag 배열에서 2 정점을 True(방문) 처리하고, 떠나온 0 정점은 다시 돌아가기 위한 발자국으로 남기기 위해서 스택에 넣는다.

위와 마찬가지 과정을 통해 2 정점을 떠나면서 스택에 2 정점을 넣고, 3 정점을 방문한 뒤 방문 Flag 배열의 3 정점에 대한 방문 여부를 True로 변경한다.

또 마찬가지로 같은 과정을 반복하는데 3 정점에서는 1 정점과 4 정점에 접근 가능하다 어디로 가든 상관없지만 이번 예에서는 4 정점에 방문할 것이다.

4 정점에서는 인접한 정점이 모두 방문 처리 되었으므로 이제 스택에서 값을 POP 함으로써 되돌아 가면서 그냥 지나친 정점을 탐색한다.

3 정점으로 돌아왔을 때, 보니까 1 정점을 방문하지 않고 그냥 지나쳤었기 때문에 1 정점에 방문한다. 이 때, 1 정점에 방문하기 위해서 3 정점을 떠나는 것이니 1 정점 방문 이후 다시 돌아오기 위해 3 정점을 다시 스택에 넣는다. 그리고 1 정점에 대한 방문 처리를 진행한다.

그리고 1 정점에서 인접 정점 모두 방문 처리 되었으니 Pop을 통해 돌아가고, 3 정점에서도, 2 정점에서도 마찬가지로 인접 정점 모두 방문처리 되었으므로 Pop을 통해 돌아가다가 0 시작 정점까지 Pop하여 스택이 빈 경우 비로소 모든 순회가 끝난 것이다.

0 -> 2 -> 3 -> 4 -> 1 순으로 순회가 이루어졌다.

진짜 뇌리에 박히겠다 박히겠어 정말 ㅋㅋ

이제 관련된 부분 코드를 보도록 하겠다.

코드 분석

스택이 새롭게 사용되므로 스택에 대한 코드가 필요한데 이미 만들어놓았던 배열 기반의 스택 코드를 활용할 것이다. 스택 설명 기록은 아래의 링크에서 확인하면 된다.

먼저 바뀌는 부분과 추가되는 부분이다.

그래프 내의 방문 Flag 배열이 추가 된다.

방문 처리를 수행하는 함수가 추가된다.

깊이 우선 탐색을 수행하는 함수이다.

한 함수이지만 라인 수를 맞춰서 읽으면 된다... 이전 자료구조인 스택에 대한 사용 방법 또한 익혀야 하고 너무나도 추상적이라서 용어 설명이 너무 어려운 것 같다..ㅠ.ㅠ

그래프 종료 및 메모리 공간 해체 관련 코드이다.

전체 코드 및 실행 결과

전체 코드는 배열 기반의 스택과 변형된 연결리스트(오름차순으로 노드를 삽입; 이전에는 그냥 삽입했다.), DFS로 인해 변경된 그래프 코드 순으로 업로드 한다.

배열 기반의 스택 ArrayBasedStack.h -- -- -- -- --

변형된 연결 리스트 linkedlistforgraph.h -- -- -- -- --